A cubical transparent slab is used as a paper weight. What should be the minimum refractive index of the material of the slab so that letters below it are not visible from any of its vertical faces.
√2
√3
√5
√5/√3
To solve the problem of determining the minimum refractive index of a cubical transparent slab so that letters below it are not visible from any of its vertical faces, we can follow these steps:
1. Understanding the Geometry of the Slab:
- Let the side length of the cube be denoted as L.
- The light must travel through the slab and exit from the vertical faces without being visible.
2. Identifying the Path of Light:
- The critical condition for the letters to be invisible is that the light exiting the slab must be at the critical angle. This means that the light will travel diagonally through the cube.
3. Calculating the Diagonal of the Cube:
- The diagonal d of the cube can be calculated using the formula:
d=L√2
4. Applying Snell's Law:
- According to Snell's Law:
n1sin(θ1)=n2sin(θ2)
- Here, n1 is the refractive index of the slab, n2 is the refractive index of air (which is 1), θ1 is the angle of incidence, and θ2 is the angle of refraction.
5. Setting Up for Critical Angle:
- For the light to exit horizontally, the angle of refraction θ2 must be 90∘, thus sin(θ2)=1.
- The angle of incidence θ1 must equal the critical angle θc.
6. Using the Critical Angle:
- From Snell's Law, we can write:
n1sin(θc)=1
- Rearranging gives:
n1=1sin(θc)
7. Finding the Critical Angle:
- The critical angle can be found using the geometry of the cube. The opposite side to the angle θc is L, and the hypotenuse (the diagonal) is L√2.
- Thus:
sin(θc)=LL√2=1√2
8. Calculating the Minimum Refractive Index:
- Substituting this back into the equation for n1:
n1=11√2=√2
9. Conclusion:
- The minimum refractive index of the material of the slab so that letters below it are not visible from any of its vertical faces is:
n=√2
- Let the side length of the cube be denoted as L.
- The light must travel through the slab and exit from the vertical faces without being visible.
- The critical condition for the letters to be invisible is that the light exiting the slab must be at the critical angle. This means that the light will travel diagonally through the cube.
- The diagonal d of the cube can be calculated using the formula:
d=L√2
- According to Snell's Law:
n1sin(θ1)=n2sin(θ2)
- Here, n1 is the refractive index of the slab, n2 is the refractive index of air (which is 1), θ1 is the angle of incidence, and θ2 is the angle of refraction.
- For the light to exit horizontally, the angle of refraction θ2 must be 90∘, thus sin(θ2)=1.
- The angle of incidence θ1 must equal the critical angle θc.
- From Snell's Law, we can write:
n1sin(θc)=1
- Rearranging gives:
n1=1sin(θc)
- The critical angle can be found using the geometry of the cube. The opposite side to the angle θc is L, and the hypotenuse (the diagonal) is L√2.
- Thus:
sin(θc)=LL√2=1√2
- Substituting this back into the equation for n1:
n1=11√2=√2
- The minimum refractive index of the material of the slab so that letters below it are not visible from any of its vertical faces is:
n=√2
Similar Questions
What should be the minimum value of refractive index of a prism, refracting angle A, so that there is no emergent ray irrespective of the angle of incidence?

View SolutionLight enters at an angle of incidence in a transparent rod of refractive index n. For what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face whatsoever be the value of angle of incidence.
View Solution
Knowledge Check
A point source of light is placed at a depth of h below the surface of water of refractive index μ. A floating opaque disc is placed on the surface of water so that light from the source is not visible from the surface. The minimum diameter of the disc is
A2h(μ2−1)1/2B2h(μ2−1)1/2Ch2(μ2−1)1/2Dh(μ2−1)1/2
Light enters at an angle of incidence in a transparent rod of refractive index n. For what value of the refractive index of the material of the rod the light once entered into it will not leave it through its lateral face whatsoever be the value of angle of incidence.
View SolutionA rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
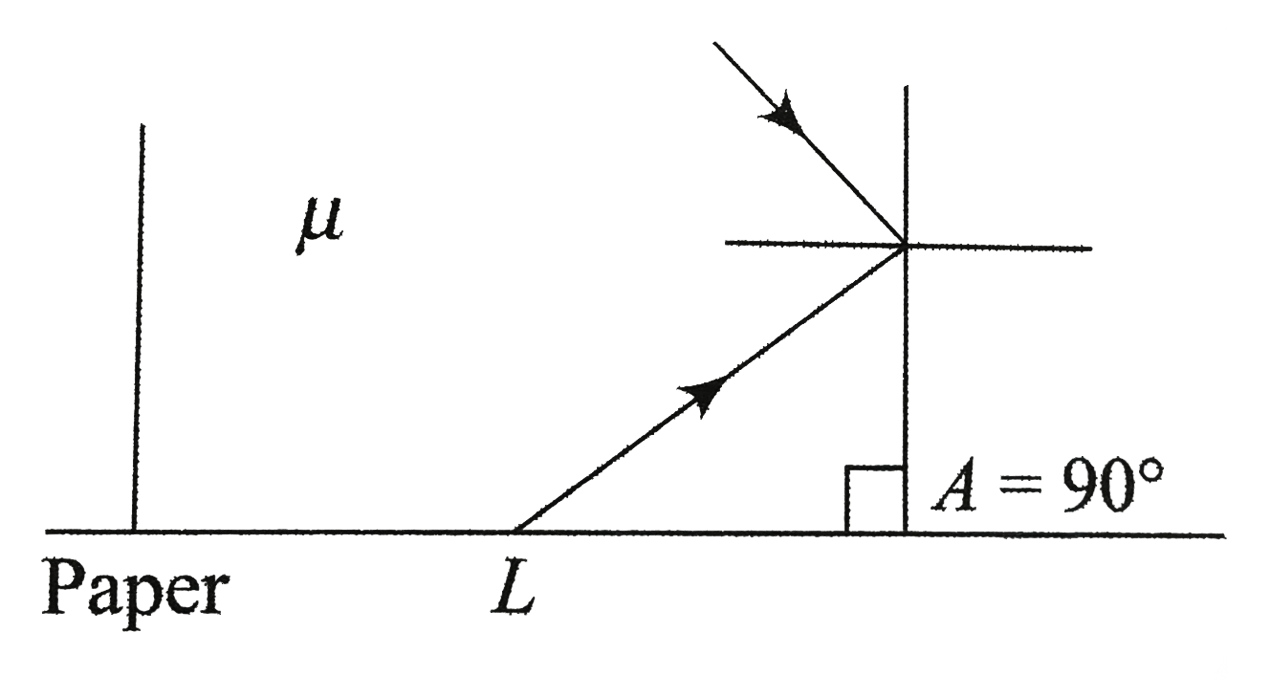
View SolutionA ray of light falls on an equilateral prism ABC as shown. Face AC of the prism is polished.

What is the refractive index μ of the material of the prims so that when the ray falls on face BC (after reflecting from AC) it makes an angle 60∘ with it.?
View SolutionA glass slab of thickness 2cm and refractive index 2 is placed in contact with a biconvex lens of focal length 20cm. The refractive index of the material of the lens 1.5 . The far side of the lens is silvered. Where should an object be placed in front of the slab so that it images on to itself?
View SolutionTwo transparent slabs having equal thickness but different refractive indices μ1andμ2, are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits ?
View SolutionAn object is placed at f/2 away from first focus of a convex lens where f is the focal length of the lens. Its image is formed at a distance 3f/2 in a slab of refractive index 3/2 , from the face of the slab facing the lens. Find the distance of this face of the slab from the second focus of the lens.

View SolutionThe refractive index of the material of a prism of refracting angle 45∘ is 1.6 for a certain monochromatic ray. What will be the minimum angle of incidence of this ray on the prism so that no TIR takes place as the ray comes out of the prism.
View Solution
