If a ray of light takes t1 and t2 times in two media of absolute refractive indices μ1 and μ2 respectively to travel same distance, then
μ1t1=μ2t2
μ1t2=μ2t1
t1√μ1=t2√μ2
t1√μ2=t2√μ1
The correct Answer is:B
To solve the problem, we need to establish the relationship between the refractive indices of two media and the times taken by light to travel the same distance in those media.
1. Understanding the Problem:
We have two media with absolute refractive indices μ1 and μ2. A ray of light takes time t1 to travel a distance d in the first medium and time t2 to travel the same distance d in the second medium.
2. Using the Formula for Refractive Index:
The refractive index μ of a medium is defined as:
μ=cv
where c is the speed of light in vacuum and v is the speed of light in the medium.
3. Calculating Speed in the First Medium:
The speed of light in the first medium can be expressed as:
v1=dt1
Substituting this into the refractive index formula gives:
μ1=cv1=cdt1=c⋅t1d
Rearranging this, we get:
μ1t1=cd(Equation 1)
4. Calculating Speed in the Second Medium:
Similarly, for the second medium, the speed of light can be expressed as:
v2=dt2
Thus, the refractive index for the second medium is:
μ2=cv2=cdt2=c⋅t2d
Rearranging this gives:
μ2t2=cd(Equation 2)
5. Equating the Two Equations:
From Equations 1 and 2, we have:
μ1t1=μ2t2
This can be rearranged to give:
μ1⋅t2=μ2⋅t1
6. Final Result:
Thus, the relationship between the refractive indices and the times taken is:
μ1μ2=t1t2
We have two media with absolute refractive indices μ1 and μ2. A ray of light takes time t1 to travel a distance d in the first medium and time t2 to travel the same distance d in the second medium.
The refractive index μ of a medium is defined as:
μ=cv
where c is the speed of light in vacuum and v is the speed of light in the medium.
The speed of light in the first medium can be expressed as:
v1=dt1
Substituting this into the refractive index formula gives:
μ1=cv1=cdt1=c⋅t1d
Rearranging this, we get:
μ1t1=cd(Equation 1)
Similarly, for the second medium, the speed of light can be expressed as:
v2=dt2
Thus, the refractive index for the second medium is:
μ2=cv2=cdt2=c⋅t2d
Rearranging this gives:
μ2t2=cd(Equation 2)
From Equations 1 and 2, we have:
μ1t1=μ2t2
This can be rearranged to give:
μ1⋅t2=μ2⋅t1
Thus, the relationship between the refractive indices and the times taken is:
μ1μ2=t1t2
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:CUQ (LENS MAKER’S FORMULA)
Explore 4 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:CUQ (PRISM)
Explore 8 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:CUQ (REFLECTION)
Explore 9 Videos
- NUCLEI Book:NARAYNAChapter:NUCLEI Exercise:ASSERTION & REASON
Explore 5 Videos
- SEMI CONDUCTOR DEVICESBook:NARAYNAChapter:SEMI CONDUCTOR DEVICESExercise:Level-II (H.W)
Explore 36 Videos
Similar Questions
A meniscus lens is made of a material of refractive index μ2.Both its surfaces have radii of curvature R.It has two different media of refractive indices μ1and μ3 respectively ,on its two sides (See figure) .Calcualte its focal length for μ1<μ2<μ3,when light is incidence on it as shown
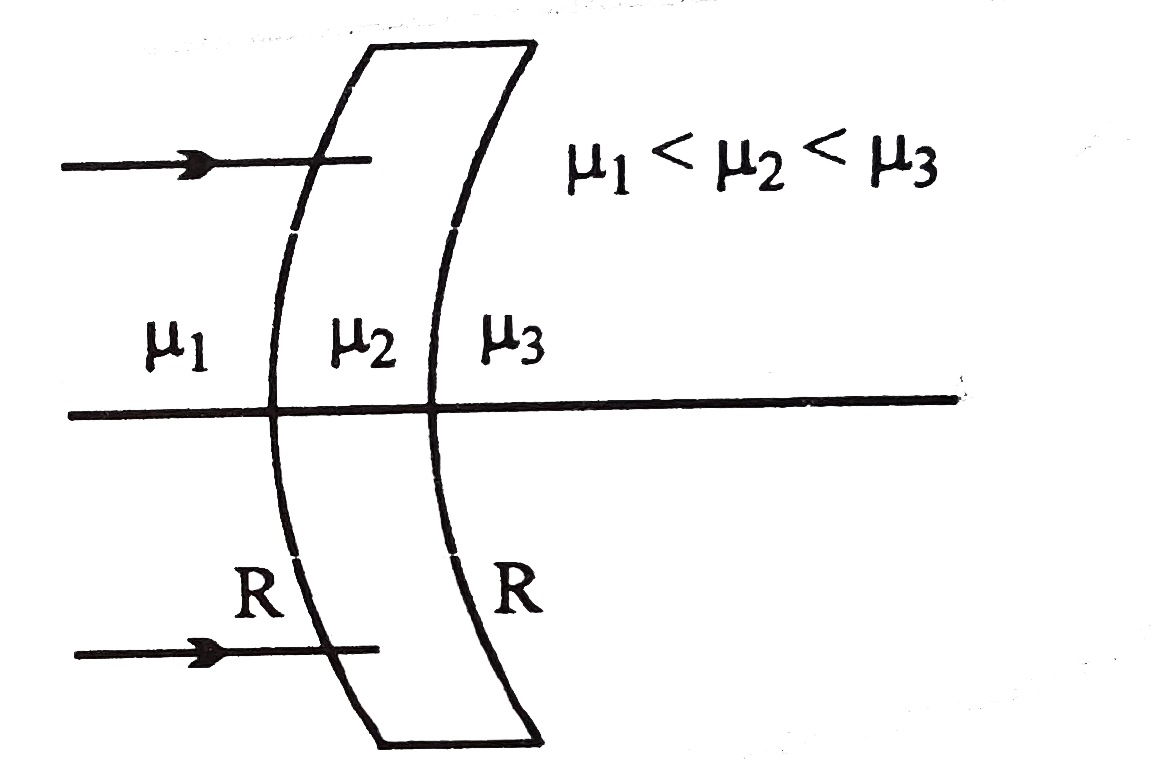
View SolutionIn the figure below, PQRS denotes the path followed by a ray of light as it travels through three media in succession. The absolute refractive indices of the media are μ1 ,mu_(2)andmu_(3) respectively. (The line segment RS' in the figure is parallel to PQ).

View Solution
Knowledge Check
If refractive index of core & cladding are μ1 & μ2 respectively then :
Aμ1>μ2Bμ2>μ1Cμ1=μ2DNone of theseIf refractive index of core & cladding are μ1&μ2 respectively then :
Aμ1>μ2Bμ2>μ1Cμ1=μ2DNone of theseIf μ1andμ2are aboslute refractive index of medium 1 and medium 2 respectively, then
A1μ2=μ1μ2B1μ2=μ2μ1C1μ2=μ1μ2D1μ2=1μ1μ2
If the figure below, PQRS denotes the path followed by a ray of light as it travels three media in succession. The absoulte refractive indices of the media are μ1,μ2 and μ3 respectively (The line segment RS' in the figure is parallel to PQ) Then :
 .
.
View SolutionThe length of the optical path of two media in contact of length d1 and d2 of refractive indices μ1 and μ2 respectively, is
View SolutionThe length of the optical path of two media in contact of length d1 and d2 of refractive indices μ1 and μ2 respectively, is
View SolutionIf the behaviour of light rays is as shown in the figure. The relation between refractive indices μ,μ1 "and" μ2 is
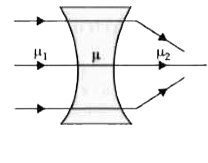
View SolutionThe length of the optical path of two media in contact of length d1 and d2 of refreactive indices μ1 and μ2 respectively, is
View Solution
