When a ray of light enters from one medium to another then its velocity in second medium becomes doubled. The maximum value of angle of incidence so that total internal reflection may not take place will be
60∘
90∘
30∘
180∘
The correct Answer is:C
To solve the problem step by step, we need to determine the maximum angle of incidence for which total internal reflection does not occur when light travels from one medium to another, given that the velocity of light in the second medium is doubled.
Step 1: Understand the relationship between velocity and refractive index
The velocity of light in a medium is given by the formula:
v=cn
where c is the speed of light in vacuum, and n is the refractive index of the medium.
Step 2: Establish the relationship between the two media
Let’s denote the refractive indices of the first and second media as n1 and n2 respectively. According to the problem, when light enters the second medium, its velocity becomes double that in the first medium. Therefore, we can write:
v2=2v1
Substituting the expressions for velocity, we have:
cn2=2(cn1)
Step 3: Simplify the equation
From the equation above, we can simplify it:
cn2=2cn1
Cancelling c from both sides gives:
1n2=2n1
Cross-multiplying yields:
n2=n12
Step 4: Apply Snell's Law for total internal reflection
Total internal reflection occurs when light travels from a medium with a higher refractive index to a medium with a lower refractive index. The critical angle θc can be found using Snell's law:
sin(θc)=n2n1
Substituting the value of n2:
sin(θc)=n12n1=12
Step 5: Calculate the critical angle
To find the critical angle θc:
θc=sin−1(12)
This gives:
θc=30∘
Step 6: Conclusion
The maximum angle of incidence for which total internal reflection does not take place is equal to the critical angle, which we have calculated to be:
θc=30∘
Final Answer
The maximum value of the angle of incidence so that total internal reflection may not take place is 30∘.
---
The velocity of light in a medium is given by the formula:
v=cn
where c is the speed of light in vacuum, and n is the refractive index of the medium.
Let’s denote the refractive indices of the first and second media as n1 and n2 respectively. According to the problem, when light enters the second medium, its velocity becomes double that in the first medium. Therefore, we can write:
v2=2v1
Substituting the expressions for velocity, we have:
cn2=2(cn1)
From the equation above, we can simplify it:
cn2=2cn1
Cancelling c from both sides gives:
1n2=2n1
Cross-multiplying yields:
n2=n12
Total internal reflection occurs when light travels from a medium with a higher refractive index to a medium with a lower refractive index. The critical angle θc can be found using Snell's law:
sin(θc)=n2n1
Substituting the value of n2:
sin(θc)=n12n1=12
To find the critical angle θc:
θc=sin−1(12)
This gives:
θc=30∘
The maximum angle of incidence for which total internal reflection does not take place is equal to the critical angle, which we have calculated to be:
θc=30∘
The maximum value of the angle of incidence so that total internal reflection may not take place is 30∘.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (H.W)(REFRACTION THROUGH SPHERICAL SURFACES)
5 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (H.W)(LENSES & THEIR COMBINATIONS)
23 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (H.W)(REFLECTION)
15 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
- SEMI CONDUCTOR DEVICESBOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)
36 Videos
Similar Questions
Knowledge Check
When a ray of light is going from one medium to another its
Aa wavelength remains sameBb frequency remains sameCc frequency increasesDd wavelength increasesTotal internal reflection can take place when light travels from
Adiamond to glassBwater to glassCair to waterDair to glassA sound wave travelling with a velocity V in a medium A reaches a point on the interface of medium A and medium B. If the velocity in the medium B be 2V, then the angle
of incidence for total internal reflection of the wave will be greater than:A15∘B30∘C45∘D90∘
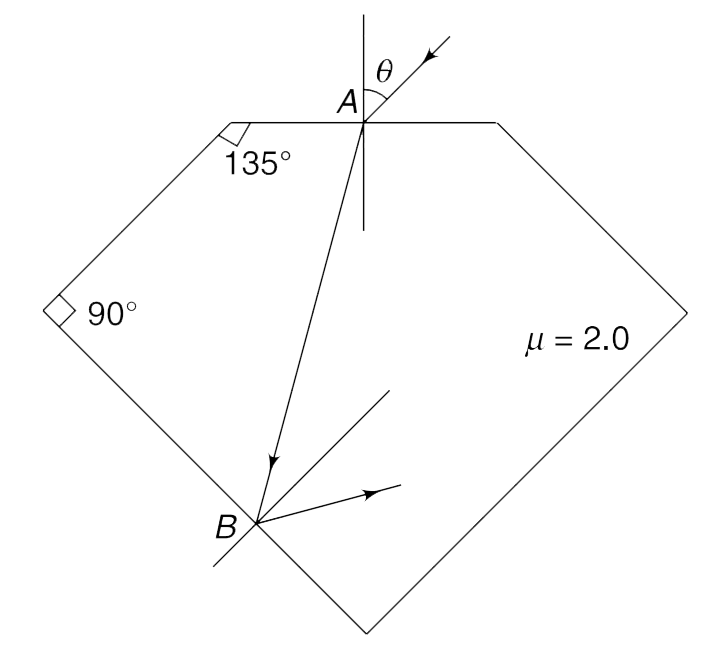
Light is incident at point A on one of the faces of a diamond crystal (μ=2.0). Find the maximum allowed value of angle of incidence θ so that light suffers total internal reflection at point B.
View SolutionWhen the ray of light travles from an optically denser medium to optically rarer medium the maximum value of angle of refraction is
View SolutionLight wave enters from medium 1 to medium 2. Its velocity in 2nd medium is double from 1st. For total internal reflection, the angle of incidence must be greater than
View SolutionThe phenomenon of change in path of ray of light when it passes from one medium to another medium is
View SolutionA ray of light gets deviated when it passes obliquely from one medium to another medium because …......................
View Solution
