Word ‘Newton’s printed on a paper and is placed on a horizontal surface below a cubical glass. The minimum value of refractive index of a cubical glass for which letters are not visible from any vertical faces, of the glass, is (Critical angle =45°)
√3
0.5
1
√2
The correct Answer is:D
To solve the problem, we need to determine the minimum value of the refractive index of a cubical glass such that the word "Newton" printed on a paper beneath it is not visible from any of the vertical faces of the glass. Given that the critical angle (θc) is 45°, we can follow these steps:
1. Understanding the Critical Angle:
The critical angle is the angle of incidence above which total internal reflection occurs. For a given refractive index n, the critical angle θc can be expressed using Snell's Law:
sin(θc)=n2n1
where n1 is the refractive index of the denser medium (glass) and n2 is the refractive index of the rarer medium (air, which is approximately 1).
2. Setting Up the Equation:
Since θc=45∘, we have:
sin(45∘)=1√2≈0.707
Therefore, substituting into the equation:
1√2=1n1
Rearranging gives:
n1=√2
3. Interpreting the Result:
The refractive index n1 of the glass must be at least √2 (approximately 1.414) for the light rays coming from the letters to undergo total internal reflection. This means that no light can escape through the vertical faces of the glass, making the letters invisible.
4. Conclusion:
The minimum value of the refractive index of the cubical glass for which the letters "Newton" are not visible from any vertical face is:
n1=√2
Final Answer:
The minimum value of the refractive index of the cubical glass is √2.
---
The critical angle is the angle of incidence above which total internal reflection occurs. For a given refractive index n, the critical angle θc can be expressed using Snell's Law:
sin(θc)=n2n1
where n1 is the refractive index of the denser medium (glass) and n2 is the refractive index of the rarer medium (air, which is approximately 1).
Since θc=45∘, we have:
sin(45∘)=1√2≈0.707
Therefore, substituting into the equation:
1√2=1n1
Rearranging gives:
n1=√2
The refractive index n1 of the glass must be at least √2 (approximately 1.414) for the light rays coming from the letters to undergo total internal reflection. This means that no light can escape through the vertical faces of the glass, making the letters invisible.
The minimum value of the refractive index of the cubical glass for which the letters "Newton" are not visible from any vertical face is:
n1=√2
The minimum value of the refractive index of the cubical glass is √2.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (H.W)(REFRACTION THROUGH SPHERICAL SURFACES)
5 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (H.W)(LENSES & THEIR COMBINATIONS)
23 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - EXERCISE-2 (H.W)(REFLECTION)
15 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
- SEMI CONDUCTOR DEVICESBOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)
36 Videos
Similar Questions
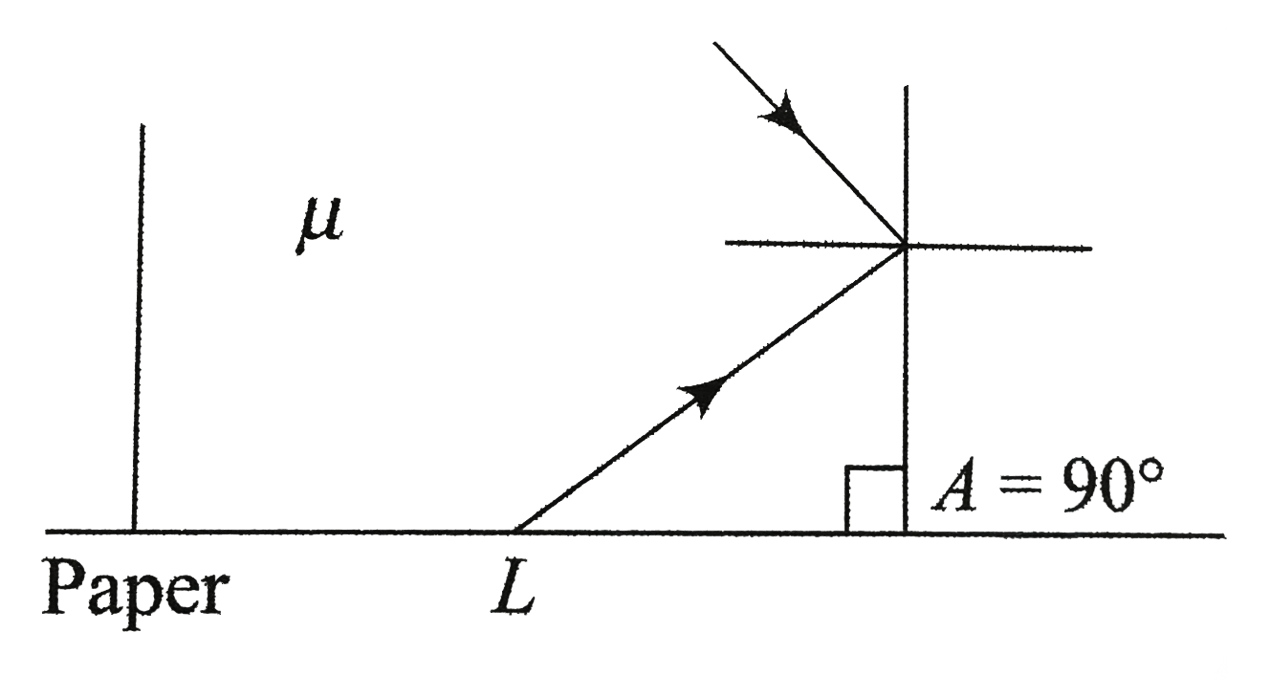
A rectangulat block of refractive index μ is placed on a printed page lying on a horizontal surface as shown in Fig. , Find the minimum value of μ so that the letter L on the page is not visible from any of the vertical sides.
View SolutionLight reflected from the surface of glass plate of refractive index 1.57 is linearly polarised. Calculate the angle of refraction in glass.
View Solution
Knowledge Check
A cubical transparent slab is used as a paper weight. What should be the minimum refractive index of the material of the slab so that letters below it are not visible from any of its vertical faces.
A√2B√3C√5D√5/√3In the figure shown , for an angle of incidence 45∘, at the top surface , what is the minimum refractive index needed for the internal reflection at vertical face ?
 A√2+12B√3/2C√1/2D√2+1
A√2+12B√3/2C√1/2D√2+1A glass prism of refractive index 1.5 is placed in water of refractive index 1.33. The minimum value of the angle of the prism so that it will not be possible to have any emergent ray is
A150∘B125∘C165∘D180∘
A ray of light incident on the horizontal surface of a glass slab at 70∘ just grazes the adjacent vertical surface after refraction. Complete the critical angle and refractive index of glass.
View SolutionA point object is placed at the centre of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View SolutionA point object is placed at the centre of a glass sphere of radius 6 cm and refractive index 1.5. The distance of the virtual image from the surface of the glass is
View SolutionIn the figure shown , for an angle of incidence 45∘, at the top surface , what is the minimum refractive index needed for the internal reflection at vertical face ?

View SolutionA point object is placed at the center of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View Solution
