A particle moves for 8s. It first accelerates from rest and then retards to rest. If the re tardation be 3 times the acceleration, then 1 time for which it accelerates will be
2s
3s
4s
6s
The correct Answer is:D
To solve the problem step by step, we can follow these instructions:
Step 1: Define Variables
Let:
- t1 = time for which the particle accelerates
- t2 = time for which the particle decelerates
- a = acceleration
- d = retardation (deceleration)
Given that the retardation d is 3 times the acceleration a:
d=3a
Step 2: Write the Total Time Equation
The total time of motion is given as 8 seconds:
t1+t2=8
Step 3: Relate Acceleration and Deceleration Times
Since the particle accelerates for t1 seconds and then decelerates for t2 seconds, we can relate t1 and t2 using the relationship of acceleration and retardation. The final velocity after acceleration will be:
v=a⋅t1
During deceleration, the initial velocity is v and the final velocity is 0. The equation for deceleration can be expressed as:
0=v−d⋅t2
Substituting d=3a into the equation gives:
0=a⋅t1−3a⋅t2
Dividing through by a (assuming a≠0):
0=t1−3t2
Thus, we can express t1 in terms of t2:
t1=3t2
Step 4: Substitute into Total Time Equation
Now substitute t1=3t2 into the total time equation:
3t2+t2=8
This simplifies to:
4t2=8
Step 5: Solve for t2
Now, solve for t2:
t2=84=2 seconds
Step 6: Find t1
Now substitute t2=2 back into the equation for t1:
t1=3t2=3⋅2=6 seconds
Final Answer
The time for which the particle accelerates is:
t1=6 seconds
---
Let:
- t1 = time for which the particle accelerates
- t2 = time for which the particle decelerates
- a = acceleration
- d = retardation (deceleration)
d=3a
The total time of motion is given as 8 seconds:
t1+t2=8
Since the particle accelerates for t1 seconds and then decelerates for t2 seconds, we can relate t1 and t2 using the relationship of acceleration and retardation. The final velocity after acceleration will be:
v=a⋅t1
During deceleration, the initial velocity is v and the final velocity is 0. The equation for deceleration can be expressed as:
0=v−d⋅t2
Substituting d=3a into the equation gives:
0=a⋅t1−3a⋅t2
Dividing through by a (assuming a≠0):
0=t1−3t2
Thus, we can express t1 in terms of t2:
t1=3t2
Now substitute t1=3t2 into the total time equation:
3t2+t2=8
This simplifies to:
4t2=8
Now, solve for t2:
t2=84=2 seconds
Now substitute t2=2 back into the equation for t1:
t1=3t2=3⋅2=6 seconds
The time for which the particle accelerates is:
t1=6 seconds
Similar Questions
A particle is moving on a circular path of radius 1m. It starts from rest,its tangential acceleration is √3t .The time after which the acceleration of the particle makes an angle of 30∘ with centripetal acceleration is (n)23s .Find the value of n.
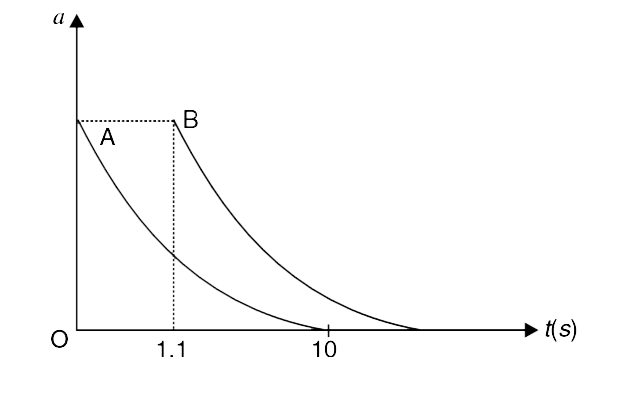
View SolutionParticle A starts from rest and moves along a straight line. Acceleration of the particle varies with time as shown in the graph. In 10 s the velocity of the particle becomes 60m/s and the acceleration drops to zero. Another particle B starts from the same location at time t=1.1s and has acceleration – time relationship identical to A with a delay of 1.1s. Find distance between the particles at time t=15s.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A body starts from rest and then moves with uniform acceleration. Then.
AIts displacement is directly proportional to square of timeBIts displacement is inversely proportion to the square of the time.CIt may move along a circle.DIt always moves in a straight line. - Question 2 - Select One
A body travels a distance s in t seconds. It starts from rest and ends at rest . In the first part of the journey , it moves with constant acceleration f and in the second part with constant retardation r. the value of t is given by
A√8s(1f+1r)B2s(1f+1r)C2s1f+1rD√2s(f+r) - Question 3 - Select One
A body moves for a total of nine second starting from rest with uniform acceleration and then with uniform retardation, which is twice the value of acceleration and then stop. The duration of uniform acceleration is
A3sB4.5sC5sD6s
A particle starting from rest attains a velocity of 50ms−1 in 5 s. The acceleration of the particle is
View SolutionA particle accelerates from rest with uniform acceleration α then decelerates to rest witha constant deceleration β. Find total displacement. Given time is T
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 View Solution
View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 View Solution
View SolutionA particle is moving under constant acceleration a=kt. The motion starts from rest. The velocity and displacement as a function of time t is
View Solution

