A mass m oscillates with simple harmonic motion with frequency f=ω2π and amplitude A on a spring of stiffness constant K. Which of the following is not correct ?
The frequency is 12π√Km
The maximum velocity occurs when x = 0
The total energy of the system is 12KA2
Its minimum potential energy occurs when x = A
The correct Answer is:D
To solve the question, we need to analyze the properties of a mass oscillating in simple harmonic motion (SHM) on a spring. We are given the frequency, amplitude, and spring constant, and we need to determine which statement about the system is not correct.
1. Understanding the Basics of SHM:
- A mass m attached to a spring oscillates with simple harmonic motion (SHM). The frequency f is given by the formula:
f=ω2π
- The angular frequency ω is related to the spring constant K and mass m by:
ω=√Km
2. Equations of Motion:
- The displacement x of the mass from the mean position can be expressed as:
x(t)=Asin(ωt+ϕ)
- The maximum velocity vmax occurs when x=0 and is given by:
vmax=Aω
3. Energy in SHM:
- The total mechanical energy E in SHM is the sum of kinetic energy (KE) and potential energy (PE):
E=KE+PE
- The potential energy stored in the spring when it is displaced by x is:
PE=12Kx2
- The kinetic energy when the mass is moving with velocity v is:
KE=12mv2
4. Total Energy Calculation:
- The total energy can also be expressed in terms of amplitude A:
E=12KA2
- This energy remains constant throughout the motion.
5. Analyzing Potential Energy:
- The potential energy is maximum when the displacement x is at its maximum (i.e., x=A or x=−A).
- Conversely, the potential energy is minimum (zero) when x=0 (the mean position).
6. Identifying the Incorrect Statement:
- The question asks which statement is not correct. If a statement claims that minimum potential energy occurs at x=A, this is incorrect because:
- At x=A (maximum displacement), the potential energy is maximum, not minimum.
Conclusion:
The statement that "minimum potential energy occurs at x=A" is incorrect. Therefore, the answer to the question is that the option stating this is the one that is not correct.
- A mass m attached to a spring oscillates with simple harmonic motion (SHM). The frequency f is given by the formula:
f=ω2π
- The angular frequency ω is related to the spring constant K and mass m by:
ω=√Km
- The displacement x of the mass from the mean position can be expressed as:
x(t)=Asin(ωt+ϕ)
- The maximum velocity vmax occurs when x=0 and is given by:
vmax=Aω
- The total mechanical energy E in SHM is the sum of kinetic energy (KE) and potential energy (PE):
E=KE+PE
- The potential energy stored in the spring when it is displaced by x is:
PE=12Kx2
- The kinetic energy when the mass is moving with velocity v is:
KE=12mv2
- The total energy can also be expressed in terms of amplitude A:
E=12KA2
- This energy remains constant throughout the motion.
- The potential energy is maximum when the displacement x is at its maximum (i.e., x=A or x=−A).
- Conversely, the potential energy is minimum (zero) when x=0 (the mean position).
- The question asks which statement is not correct. If a statement claims that minimum potential energy occurs at x=A, this is incorrect because:
- At x=A (maximum displacement), the potential energy is maximum, not minimum.
The statement that "minimum potential energy occurs at x=A" is incorrect. Therefore, the answer to the question is that the option stating this is the one that is not correct.
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EVALUATE YOURSELF - 35videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EVALUATE YOURSELF - 48videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EVALUATE YOURSELF - 17videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
A paricle of mass 200g executes a simple harmonic motion. The restorting force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA particle which is attached to a spring oscillates horizontally with simple harmonic motion with a frequency of 1/π Hz and total energy of 10J. If the maximum speed of the particle is 0.4ms−1, what is the force constant of the spring? What will be the maximum potential energy of the spring during the motion?
View Solution
Knowledge Check
- Question 1 - Select One
A mass m oscillates with simple harmonic motion with frequency f=ω2πand amlitude A on a spring with constant K. therefore
Athe total energy of the system is 12KA2BThe frequency is 12π√KMCThe maximum velocity occurs, when x=0Dall the above are correct - Question 2 - Select One
The mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is
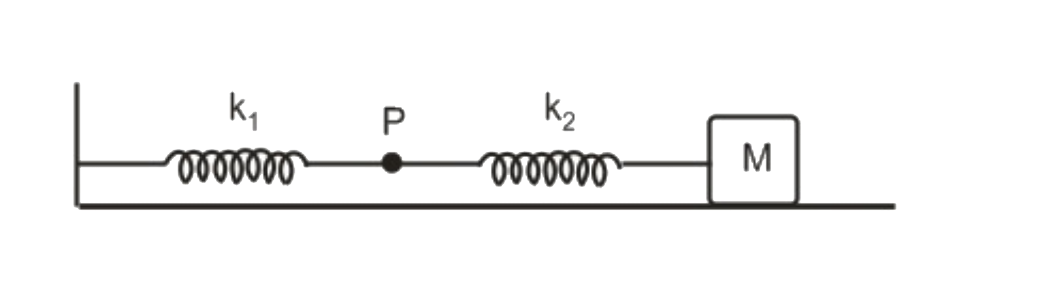 Ak1Ak2Bk2Ak2−k1Ck2Ak1+k2Dk2Ak1
Ak1Ak2Bk2Ak2−k1Ck2Ak1+k2Dk2Ak1 - Question 3 - Select One
The mass M shown in the figure oscillates in simple harmnonic motion and amplitude A. The amplitude of the point P is
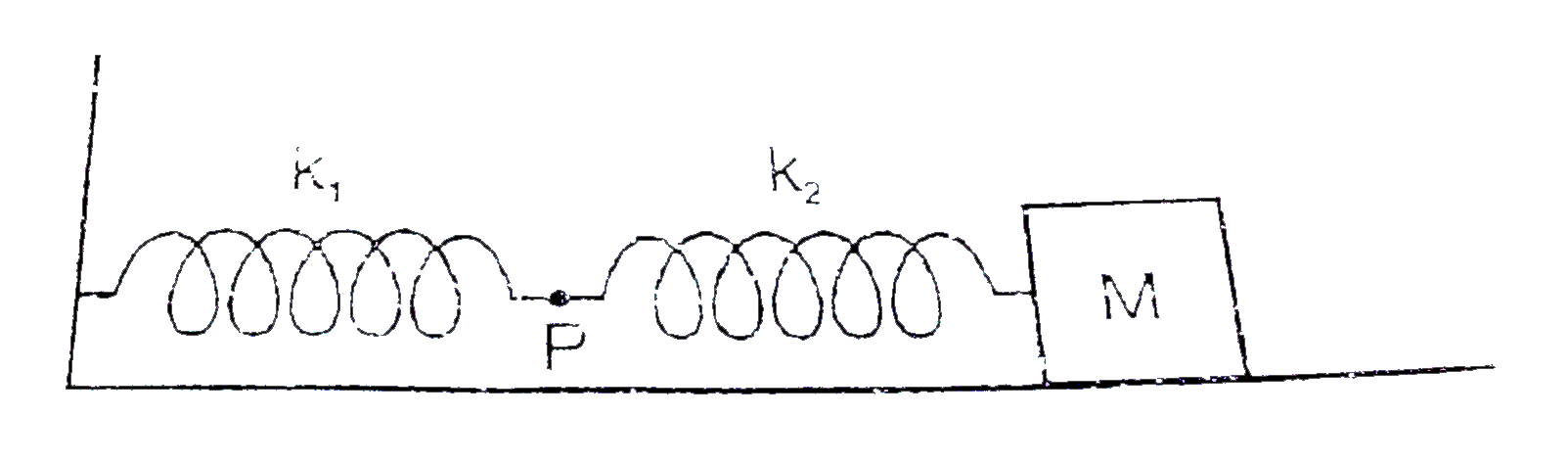 Ak1Ak2Bk2Ak1Ck1Ak1+k2Dk2Ak1+k2
Ak1Ak2Bk2Ak1Ck1Ak1+k2Dk2Ak1+k2
A ball hung from a vertical spring oscillates in simple harmonic motion with an angular frequency of 2.6 rad/s and an amplitude of 0.075m. What is the maximum acceleration of the ball?
View SolutionA particle executes simple harmonic motion with a frequency f. The frequency with which the potential. Energy oscillates is
View SolutionA man weighing 60kg stands on the horizontal platform of a spring balance. The platform starts executing simple harmonic motion of amplitude 0.1m and frequency 2πHz. Which of the following statement is correct ?
 View Solution
View SolutionA particle executes simple harmonic motion with a frequency f. The frequency with which its kinetic energy oscillates is
View SolutionA particle executes simple harmonic motion with a frequency f. The frequency with which its kinetic energy oscillates is
View Solution

