Question

A particle suspended from a vertical spring oscillates 8 times per second. At the highest point of oscillation the spring becomes unstretched. The maximum speed of the block will be

Options

A. 10 cm/s
B. 20 cm/s
C. 30 cm/s
D. 40 cm/s

Answer

B

Explanation

To find the maximum speed of the block suspended from a vertical spring oscillating at a frequency of 8 Hz, we can follow these steps:

Step 1: Identify the frequency and calculate angular frequency (ω)
The frequency (f) of the oscillation is given as 8 Hz. The angular frequency (ω) can be calculated using the formula:
\( \omega = 2\pi f \)
Substituting the value of f:
\( \omega = 2\pi \times 8 = 16\pi \text{ rad/s} \)

Step 2: Determine the amplitude (A)
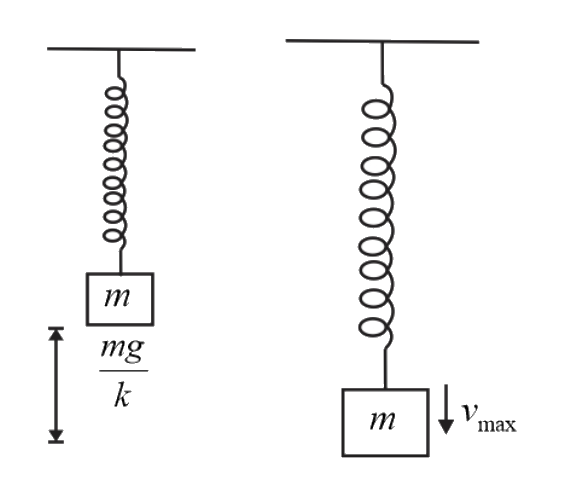
At the highest point of oscillation, the spring becomes unstretched. The maximum stretch (or amplitude, A) of the spring is when the weight of the block (mg) is balanced by the spring force (kx). Thus, we can express the amplitude as:
\( A = \frac{mg}{k} \)
Where:
- m = mass of the block
- g = acceleration due to gravity (approximately 9.81 m/s²)
- k = spring constant

Step 3: Relate angular frequency to spring constant and mass
The angular frequency (ω) is also related to the spring constant (k) and mass (m) by the formula:
\( \omega = \sqrt{\frac{k}{m}} \)
Squaring both sides gives:
\( \omega^2 = \frac{k}{m} \)
From this, we can express k as:
\( k = m\omega^2 \)

Step 4: Substitute k in the amplitude equation
Substituting the expression for k into the amplitude equation:
\( A = \frac{mg}{m\omega^2} = \frac{g}{\omega^2} \)

Step 5: Calculate maximum speed (Vmax)
The maximum speed (Vmax) in simple harmonic motion is given by:
\( V_{max} = \omega A \)
Substituting the expression for A:
\( V_{max} = \omega \left(\frac{g}{\omega^2}\right) = \frac{g}{\omega} \)

Step 6: Substitute known values
Now substituting the values of g and ω:
\( V_{max} = \frac{9.81}{16\pi} \)
Calculating this gives:
\( V_{max} \approx \frac{9.81}{50.27} \approx 0.195 m/s \)

Step 7: Convert to cm/s
To convert the maximum speed from meters per second to centimeters per second:
\( V_{max} \approx 0.195 \times 100 = 19.5 \text{ cm/s} \approx 20 \text{ cm/s} \)

Conclusion
The maximum speed of the block is approximately 20 cm/s.

---