Infinite springs with force constants k,2k,4k,8k,….. respectively are connected in series to which mass 'm' is attched. The frequency of small oscillations is……..
f=12π√2Km
f=12π√Km
f=12π√K2m
f=12π√2048Km
The correct Answer is:C
1keff=1k+12k+14k+18k+..........
=1k[1+12+14+14+18+......]
S∞=a1−r=11−12=2
1keff=1k×2⇒keff=k2
f=12π√k2m
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - I (H.W)66videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - II (C.W)27videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - C. U . Q75videos
OSCILLATIONS
- BOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION6videos
NEWTONS LAWS OF MOTION
- BOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q10videos
PHYSICAL WORLD
Similar Questions
Infinite spring with force constants k,2k,4k,8k,……..respectively are connected in series. Calculate the effetive force constant of the spring.
View SolutionInfinite springs with force constants k,2k, 4k and 8k … respectively are connected in series. What will be the effective force constant of springs, when k=10N/m
View Solution
Knowledge Check
- Question 1 - Select One
Infinite springs with force constantk , 2k, 4k and 8 k .... respectively are connected in series. The effective force constant of the spring will b
A2kBKCk/2D2048 - Question 2 - Select One
Springs of constants k, 2k, 4k, 8k,…….,2048k are connected in series. A mass m is attached to one end and the system is allowed to oscillate. The time period is approximately
A2π√m2kB2π√2mkC2π√m4kD2π√4mk - Question 3 - Select One
A spring of force constant k is cut into two equal parts, and mass 'm' is suspended from parallel combination of the springs. Then frequency of small osciollations is
Af=12π√KmBf−12π√K2mCf=12π√4KmDf=12π√2Km
Springs of spring constants k, 2k, 4k, 8k, …… are connected in series. A mass m kg is attached to the lower end of the last spring and the systemm is allowed to vibrate. What is the time period of oscillations? Given m=40gm,k=2.0Ncm−1.
View SolutionSprings of spring constant k, 2k, 4k , 8k, …. Are connected in series. A block of mass 50 kg is attached to the lower end of the last spring and the system is set into oscillation. If k = 3.0 N/cm, what is the time period of oscillations ?
View SolutionSprings of apring constants k,2k,4k,8k . . . Are connected in series. A mass m kg is attached to the lower end of the last spring and the system is allowed to vibrate. What is the time period of oscillations?
View SolutionA block of mass m is attached to three springs A,B and C having force constants k,k and 2k respectively as shown in figure. If the block is slightly oushed against spring C. If the angular frequency of oscillations is √Nkm, then find N. The system is placed on horizontal smooth surface.
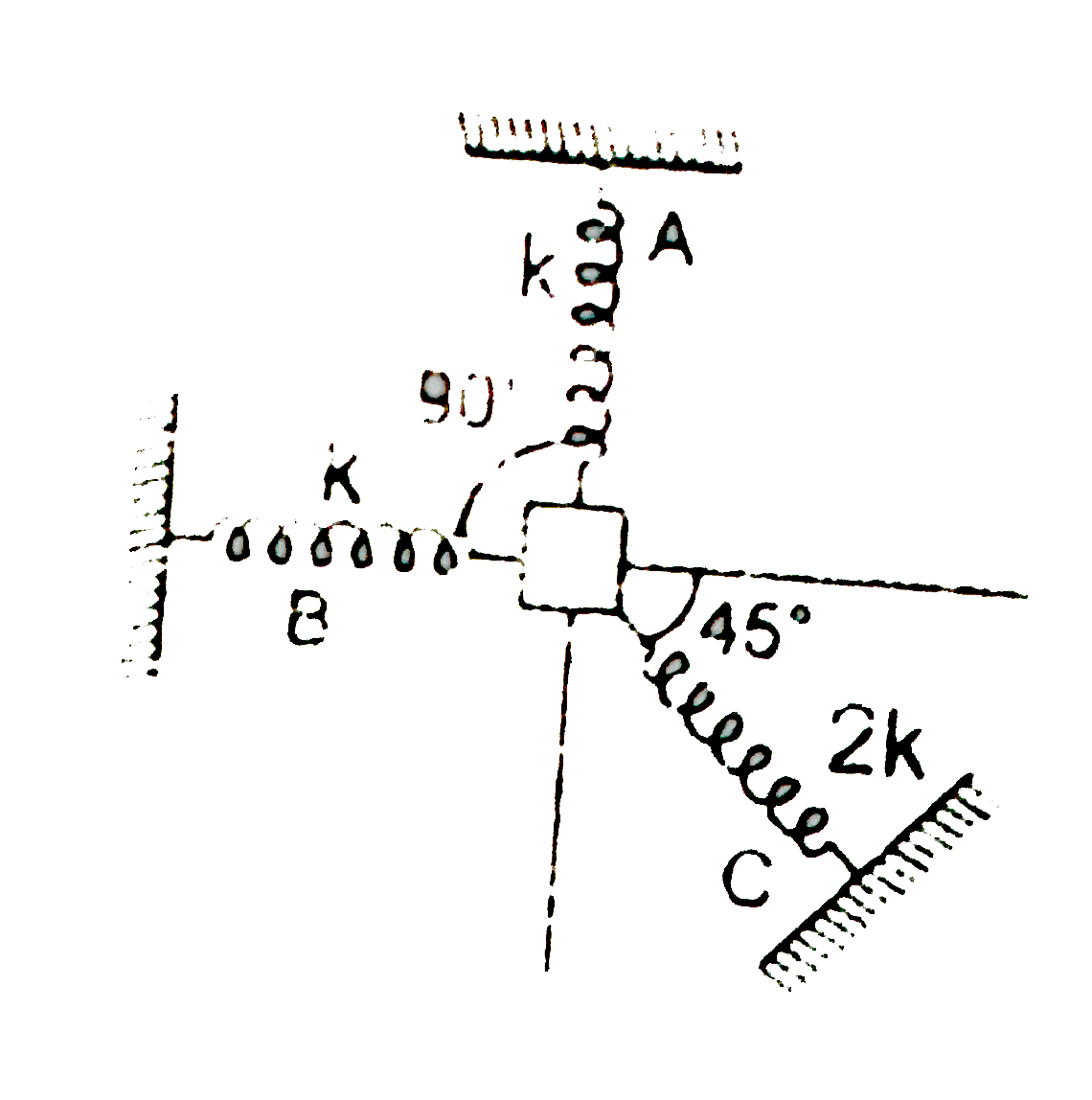 View Solution
View SolutionTwo spring of force constants K and 2K are connected a mass m below The frequency of oscillation the mass is
 View Solution
View Solution

