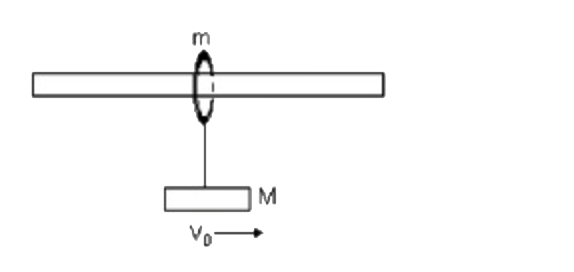
A ring of mass m free to slide on a fixed smooth horizontal rod is attached to a particle of mass M kg by a inextensible string of length l. Initially, both M and m are at rest and the string is vertical. A horizontal velocity v0 is imparted to the particle. The maximum height up to which block will rise w.r.t its initial position is (M = 2m)
v202g
v204g
v206g
v208g
The correct Answer is:C
Step by step video, text & image solution for A ring of mass m free to slide on a fixed smooth horizontal rod is attached to a particle of mass M kg by a inextensible string of length l. Initially, both M and m are at rest and the string is vertical. A horizontal velocity v_(0) is imparted to the particle. The maximum height up to which block will rise w.r.t its initial position is (M = 2m) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A smooth of mass m1 is lying on a rigid horizontal string A bob of mass m2 hangs from, the ring by an inextensible light string of length l. Find angular frequency of oscillation of the system.
View SolutionA toy car of mass m is placed on a smooth horizontal surface. A particle of mass 3m is suspended inside the car with the help of a string of length l. Initially everything is at rest. A sudden horizontal impulse I=2m√gl is applied on the car and it starts moving.
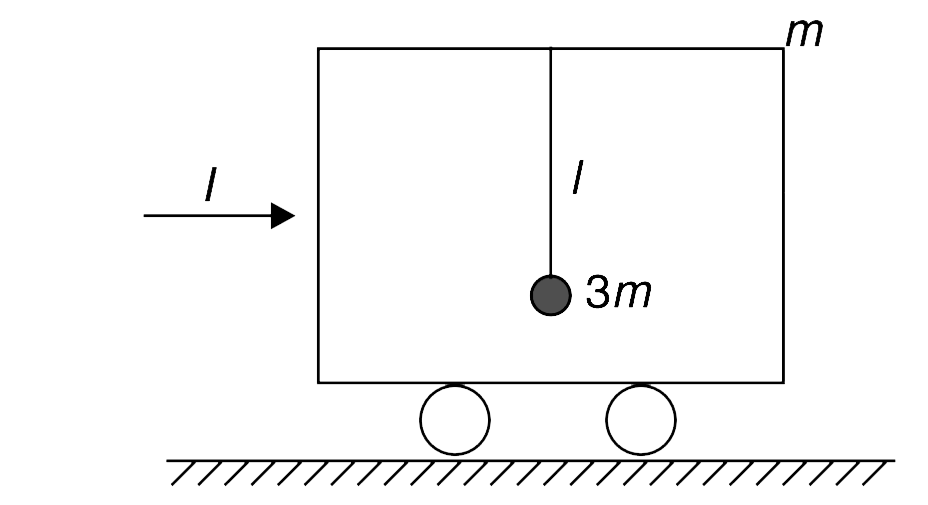
(a) Find the maximum angle q0 that the string will make with the vertical subsequently.
(b) Find tension in the string when it makes angle θ0 with the vertical.
View Solution
Knowledge Check
A mass m is hanging by a string of length l. The velocity v0 which must be imparted to it to just reach the top is
A√3glB√4glC√5glD√6glA smooth ring of mass m can slide on a fixed horizontal rod. A string tied to the ring pases over a fixed pulley B and carries a block C of mass 2m as shown below. As the ring starts sliding
 AThe acceleration of the ring is 2gcosθ1+2cos2θBThe acceleration of the block is 2g1+2cos2θCThe tension in the string is 2mg1+2cos2θDIf the block descends with velocity v then the ring slides with velocity vcosθ
AThe acceleration of the ring is 2gcosθ1+2cos2θBThe acceleration of the block is 2g1+2cos2θCThe tension in the string is 2mg1+2cos2θDIf the block descends with velocity v then the ring slides with velocity vcosθA particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
AThe string becomes slack when the partice reaches its highest pointBThe velocity of the particle becomes zero at the highest point.CThe kinetic energy of the ball in initial position was 12mv2=mgDThe particle again passes through the initial position.
Two particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be

View SolutionA uniform rod of mass m and length 2L on a smooth horizontal surface. A particle of mass m is connected to a string of length L whose other end is connected to the end ‘A’ of the rod. Initially the string is held taut perpendicular to the rod and the particle is given a velocity v0 parallel to the initial position of the rod.
(a) Calculate the acceleration of the centre of the rod immediately after the particle is projected.
(b) The particle strikes the centre of the rod and sticks to it. Calculate the angular speed of the rod after this.

View SolutionA particle of mass m suspended by a string of length l revolves in a horizontal circle (θ is the angle the string makes with vertical). Which of the following statement(s) is // are correct?
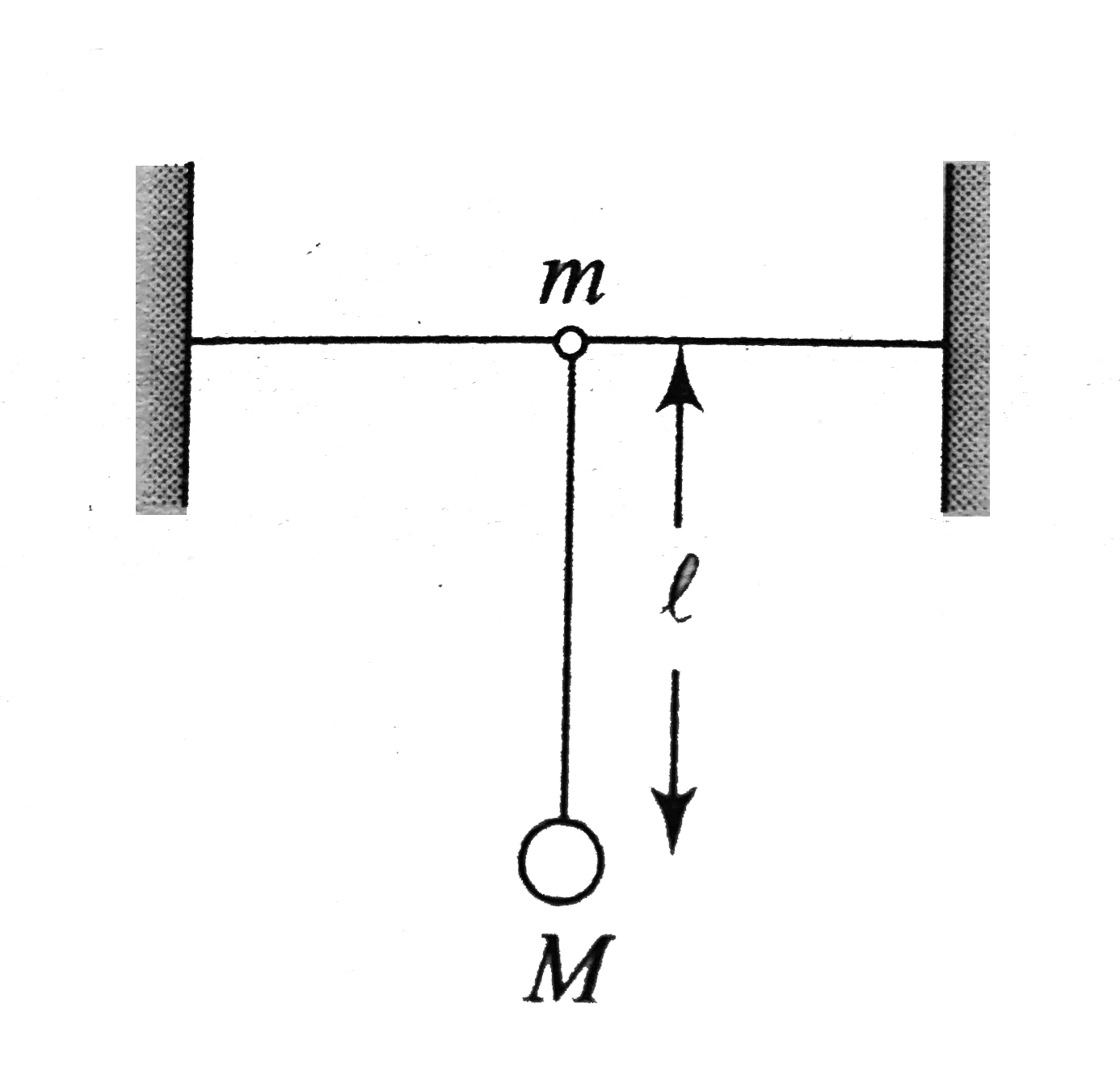
View SolutionThe ring R in the arrangement shown can slide along a smooth fixed, horizontal rod XY. It is attached to the block B by a light string. The block is released from rest, with the string horizontal. Then which of the following are true.

View SolutionA block of mass 2m is attached to a string of length L=5m. The block is released when the string is horizontal , it picks up a particle of 2m kept at rest at the lowest point. The maximum height attached by the combined mass is
View Solution