A block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. The lighter block comes to rest after collision. The loss in KE of the system is
8J
4×10−7 J
4J
0J
The correct Answer is:(3)
m1u1+m2u2=m1v1+m2v2
ΔKE=12m1u21−12m2v22
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE -II (C.W)75videos
WORK , ENERGY & POWER
- BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE -II (H.W)75videos
WORK , ENERGY & POWER
- BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE - 1 (C.W)70videos
WORK , ENERGY & POWER
- BOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-IV56videos
WAVES
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-VI (Integer)12videos
WORK POWER AND ENERGY
Similar Questions
A block of mass m moving at speed υ collides wilth another block of mass 2 m at rest. The lighter block comes to rest after the collision. Find the coefficient of restitution.
View SolutionA spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is 2.0Nm−1 and the mass of the block is 2.0 kg. Ignore the mass of the spring. Initially the spring is in an unstretched condition. Another block of mass 1.0 kg moving with a speed of 2.0ms−1 collides elastically with the first block. The collision is such that the 2.0 kg block does not hit the wall. The distance, in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is
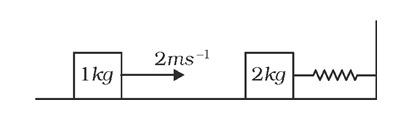 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 1kg moving with a speed of 4ms−1, collides with another block of mass 2kg which is at rest. If the lighter block comes to rest after collision, then the speed of the heavier body is
A2ms−1B1ms−1C1.5ms−1D0.5ms−1 - Question 2 - Select One
A ball of mass m moving at a speed v collides with another ball of mass 3m at rest. The lighter block comes to rest after collisoin. The coefficient of restitution is
A(a) 12B(b) 23C(c) 14D(d) None of these - Question 3 - Select One
A body of mass 4kg moving with velocity 12m/s collides with another body of mass 6kg at rest. If two bodies stick together after collision , then the loss of kinetic energy of system is
AzeroB288JC172.8JD144J
A spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is 2.0 Nm–1 and the mass of the block is 2.0 kg. Ignore the mass of the spring. Initially the spring is in an unstretched condition. Another block of mass 1.0 kg moving with a speed of 2.0 m s–1 collides elastically with the first block. The collision is such that the 2.0 kg block does not hit the wall. The distance, in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is _________.
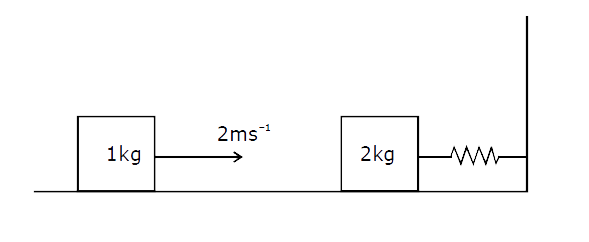 View Solution
View SolutionA body of mass 5 kg moving with a velocity 10 m/s collides with another body of the mass 20 kg at rest, and comes to rest. The velocity of the second body due to collision is
View SolutionA body of mass 5 kg moving with a velocity 10 m/s collides with another body of the mass 20 kg at, rest and comes to rest. The velocity of the second body due to collision is
View SolutionA moving block having mass m , collides with another stationary block having mass 4m. The lighter block comes to rest after collision. When the initial velocity of the block is v, then the value of coefficient of restitution (e) will be
View SolutionA moving block having mass m, collides with another stationary block having mass 4m. The lighter block comes to rest after collision. When the initial velocity of the lighter block is v, then the value of coefficient of restitution (e) will be
View Solution

