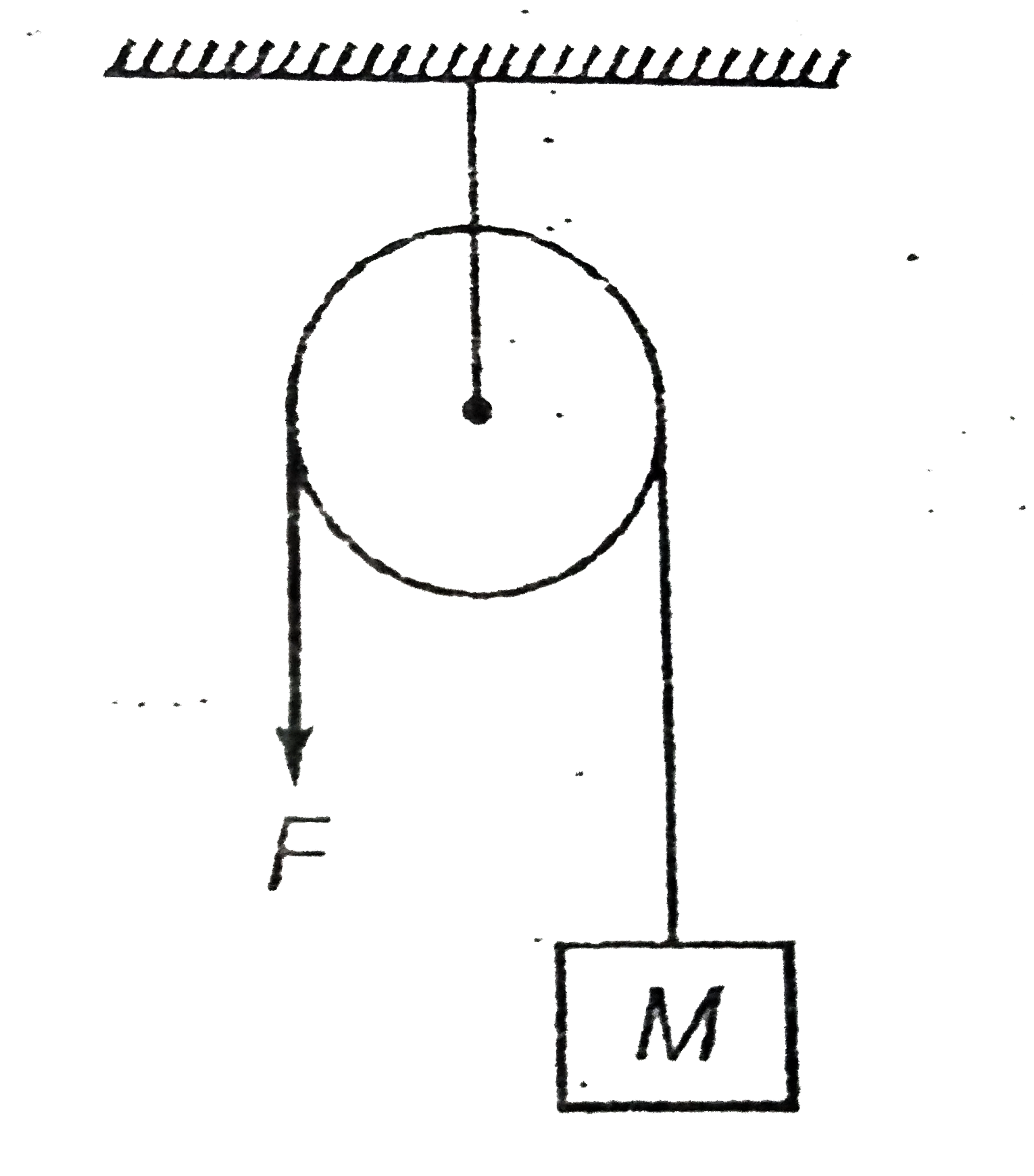
A block of mass M is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F. The kinetic energy of the block increases by 20 J in 1 s:-
The tension in the string is Mg.
The tension in the string is F
The work done by the tension on the block is 20 J in the above 1 s.
The work done by the force of gravity is 20J in the above 1 s.
The correct Answer is:(2)
To solve the problem, we need to analyze the forces acting on the block and how they relate to the change in kinetic energy.
Step 1: Understand the System
We have a block of mass M hanging from a pulley, and the other end of the string is being pulled by a constant force F. The system is in motion, and we know that the kinetic energy of the block increases by 20 J in 1 second.
Step 2: Identify Forces Acting on the Block
The forces acting on the block are:
1. The gravitational force Mg acting downwards.
2. The tension T in the string acting upwards.
Step 3: Apply Newton's Second Law
Since the block is accelerating, we can apply Newton's second law:
Net Force=mass×acceleration
The net force acting on the block can be expressed as:
T−Mg=Ma
Where a is the acceleration of the block.
Step 4: Relate Work Done to Change in Kinetic Energy
According to the work-energy theorem, the work done on the block is equal to the change in kinetic energy. The work done by the tension T and the gravitational force Mg can be expressed as:
Work Done=T⋅d−Mg⋅d
Where d is the distance moved by the block in the direction of the forces.
Step 5: Calculate the Work Done
We know that the change in kinetic energy is 20 J:
T⋅d−Mg⋅d=20
This can be rearranged to find the relationship between tension, gravitational force, and the distance moved.
Step 6: Solve for Tension
From the previous equation, we can express the tension in terms of the gravitational force and the work done:
T⋅d=Mg⋅d+20
Dividing through by d (assuming d≠0):
T=Mg+20d
Step 7: Analyze the Given Information
Since the force F is constant and equal to the tension T when the system is in equilibrium, we can conclude that:
F=T
Thus, we can substitute T from the previous step:
F=Mg+20d
Conclusion
The tension in the string is equal to the force F being applied, and the work done on the block results in an increase in kinetic energy of 20 J.
We have a block of mass M hanging from a pulley, and the other end of the string is being pulled by a constant force F. The system is in motion, and we know that the kinetic energy of the block increases by 20 J in 1 second.
The forces acting on the block are:
1. The gravitational force Mg acting downwards.
2. The tension T in the string acting upwards.
Since the block is accelerating, we can apply Newton's second law:
Net Force=mass×acceleration
The net force acting on the block can be expressed as:
T−Mg=Ma
Where a is the acceleration of the block.
According to the work-energy theorem, the work done on the block is equal to the change in kinetic energy. The work done by the tension T and the gravitational force Mg can be expressed as:
Work Done=T⋅d−Mg⋅d
Where d is the distance moved by the block in the direction of the forces.
We know that the change in kinetic energy is 20 J:
T⋅d−Mg⋅d=20
This can be rearranged to find the relationship between tension, gravitational force, and the distance moved.
From the previous equation, we can express the tension in terms of the gravitational force and the work done:
T⋅d=Mg⋅d+20
Dividing through by d (assuming d≠0):
T=Mg+20d
Since the force F is constant and equal to the tension T when the system is in equilibrium, we can conclude that:
F=T
Thus, we can substitute T from the previous step:
F=Mg+20d
The tension in the string is equal to the force F being applied, and the work done on the block results in an increase in kinetic energy of 20 J.
Topper's Solved these Questions
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE -II (H.W)
Explore 75 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE -III
Explore 54 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE -1 (H.W)
Explore 60 Videos
- WAVESBook:NARAYNAChapter:WAVESExercise:Exercise-IV
Explore 56 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Integer)
Explore 12 Videos
Similar Questions
A block of mass 10 kg is hanging over a smooth and light pulley through a light string and the other end of the string is pulled down by a constant force F. The kinetic energy of the block increases by 20 J in 1 s
View SolutionA block of mass M hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F. The kinetic of the block increases by 40J in 1s. State whether the following statements are true or false.
(a) The tension in the string is Mg .
(b) The work done the tension on the block is 40J.
(c) the tension in the string is F.
(d) The work done by the force of gravity is 40J in the above 1s .
View Solution
Knowledge Check
A block of mass M is hanging over a smooth and light pulley through a light string. The other end of the strinig is pulled by a constant force F. The kinetic energy of the block increases by 20J n 1s.
AThe tension in the string is Mg.BThe tension in the string is FCThe work done by the tension on the block is 20 J in the above 1 s.DThe work done by the force of gravity is 20J in the above 1 s.A block of mass 2 kg is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F=40N. The kinetic energy of the particle increase 40 J in a given internal of time. Then
Atension in the string is 40 NBdisplacement of the block in the given internal of time is 2 mCwork done by gravity is -20JDwork done by tension is 80 JA block of mass 2 kg is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F = 40 N. The kinetic energy of the particle increases 40 J in a given interval of time. Then, (g=10m/s2)
Atension in the string is 40 NBdisplacement of the block in the given interval of time is 2 mCwork done by gravity is −20JDwork done by tension is 80 J
A block of mass 2kg is hanging over a smooth and light pulley through a light string. The order end of the string is pulled by a constant force F=40N. The kinetic energy of the particle increase 40J in a given interval of time. Then : (g=10m/s2).
 .
.
View SolutionA block of mass 2kg is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F=40N . At t=0 the system is at rest as shown. Then in the time interval from t=0 to t=2√10 seconds, pick up the correct statement (s):(g=10m/s2)
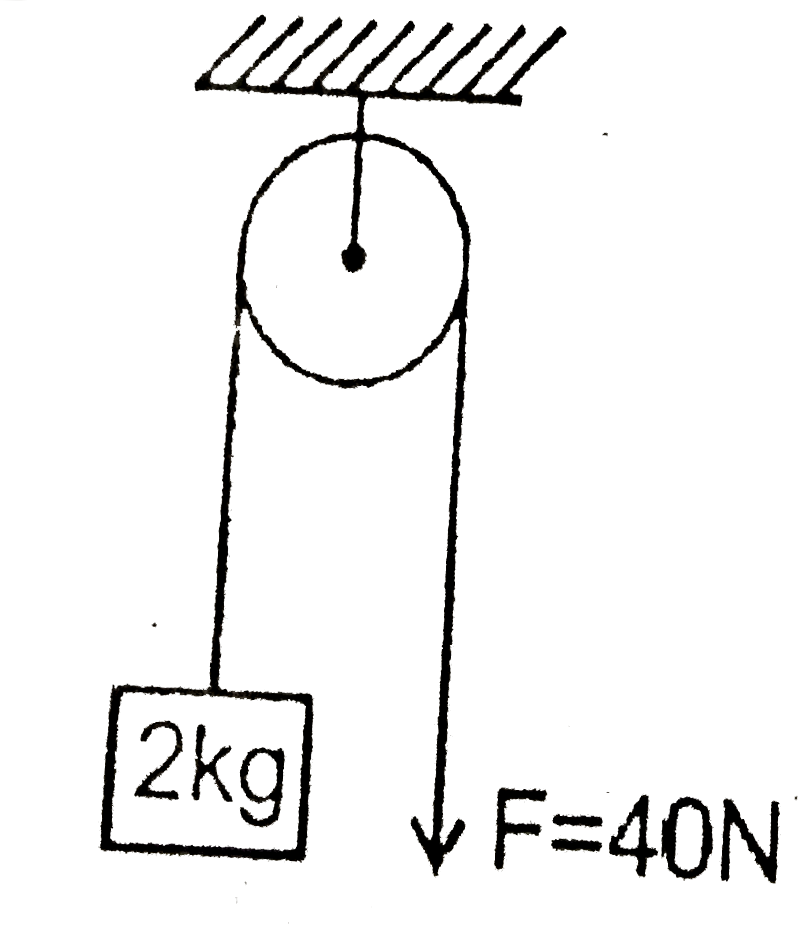
View SolutionA block of mass M is hanging over a smooth and light pulley by a constant force F. The kinetic energy of the block increases by 20 J in 1 s.
View SolutionA block of mass 2 kg is hanging from a light, smooth pulley through a light string. The kinetic energy of block increased to 16 J in 2 s by applying a constant force F on one end of upper string. Then
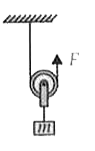
View SolutionIn the shown mass pulley system, pulleys and string are massless. The one end of the string is pulled by the force F = mg. The acceleration of the block will be :

View Solution
