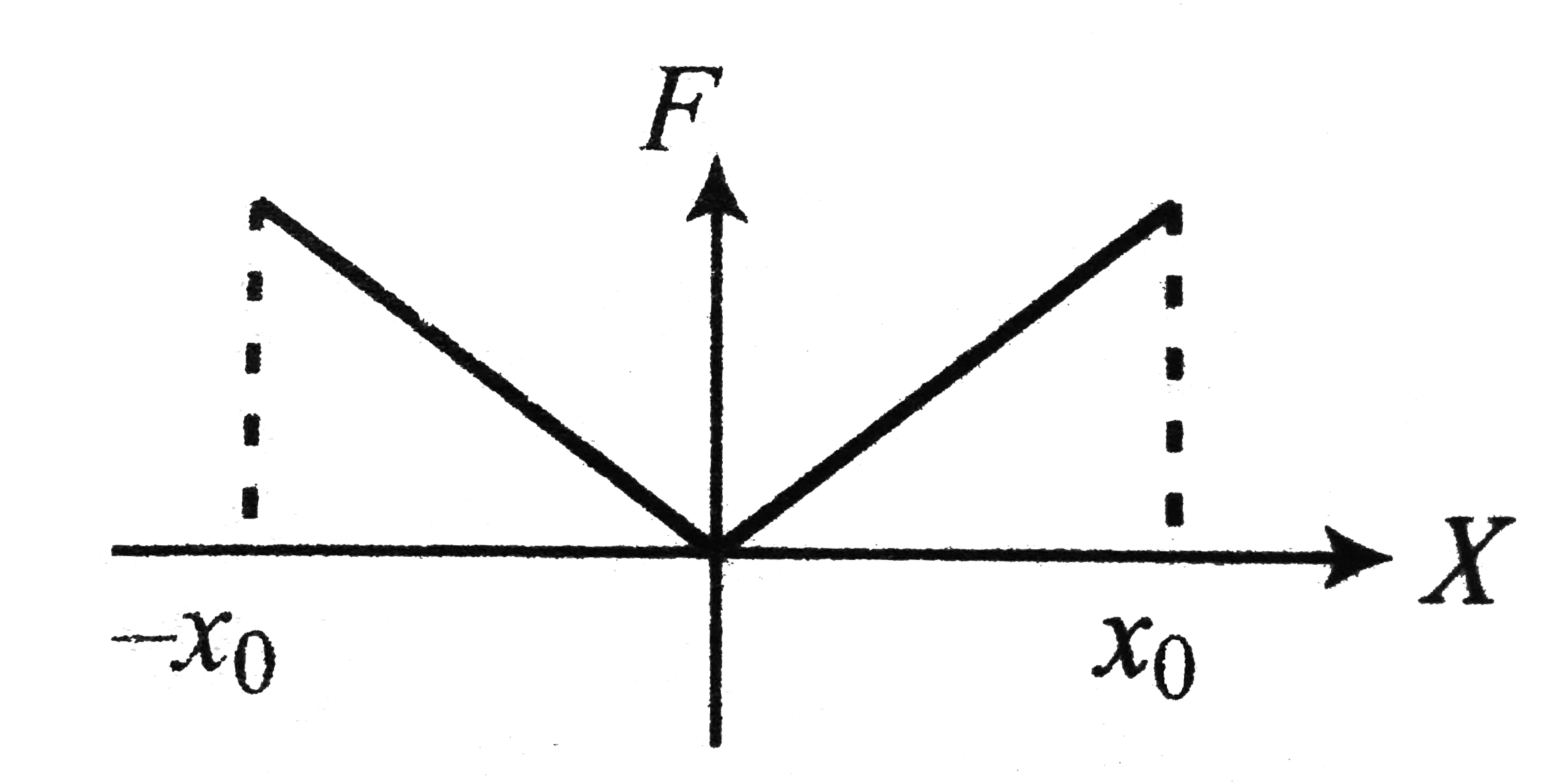
Figure given below shows the plot of the conservative force F, in a unidimensional field. The plot representing the function corresponding to the potential energy (U) in the field is :
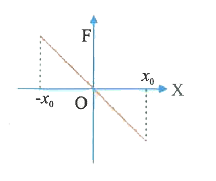
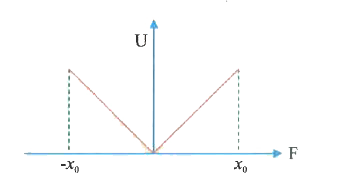
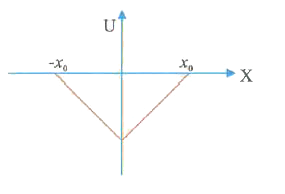


The correct Answer is:(4)
F=−dUdx⇒U=−∫Fdx=−∫(−kx)dx
U=12kx2
Which is similar to x2=4ay
Topper's Solved these Questions
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE -II (H.W)
75 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE -III
54 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE -1 (H.W)
60 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-IV
56 Videos
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-VI (Integer)
12 Videos
Similar Questions
The potential energy ‘V’ of a particle moving along the positive x-direction in a conservative force field varies as shown in the figure. The total energy is E=2. Draw the corresponding kinetic energy K vs x graph.
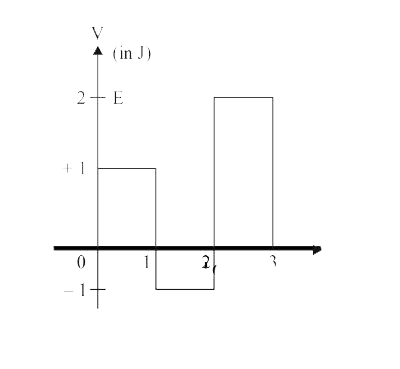
View SolutionDraw a plot of potential energy of a pair of nucleons as a function of their separation. What is the significance of negative potential energy in the graph drawn ?
View Solution
Knowledge Check
Figure shows a plot of the conservative force F in a unidimensional field. The plot representing the function corresponding to the potential energy (U) in the field is
 A
A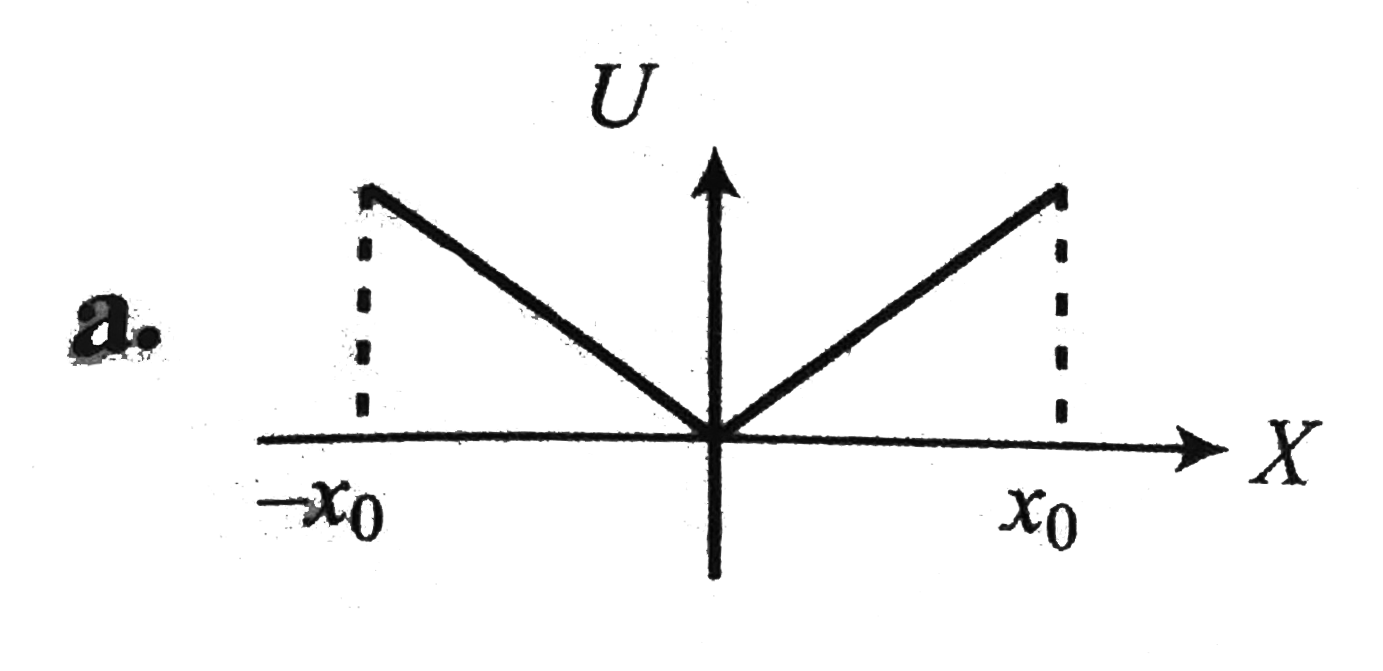 B
B C
C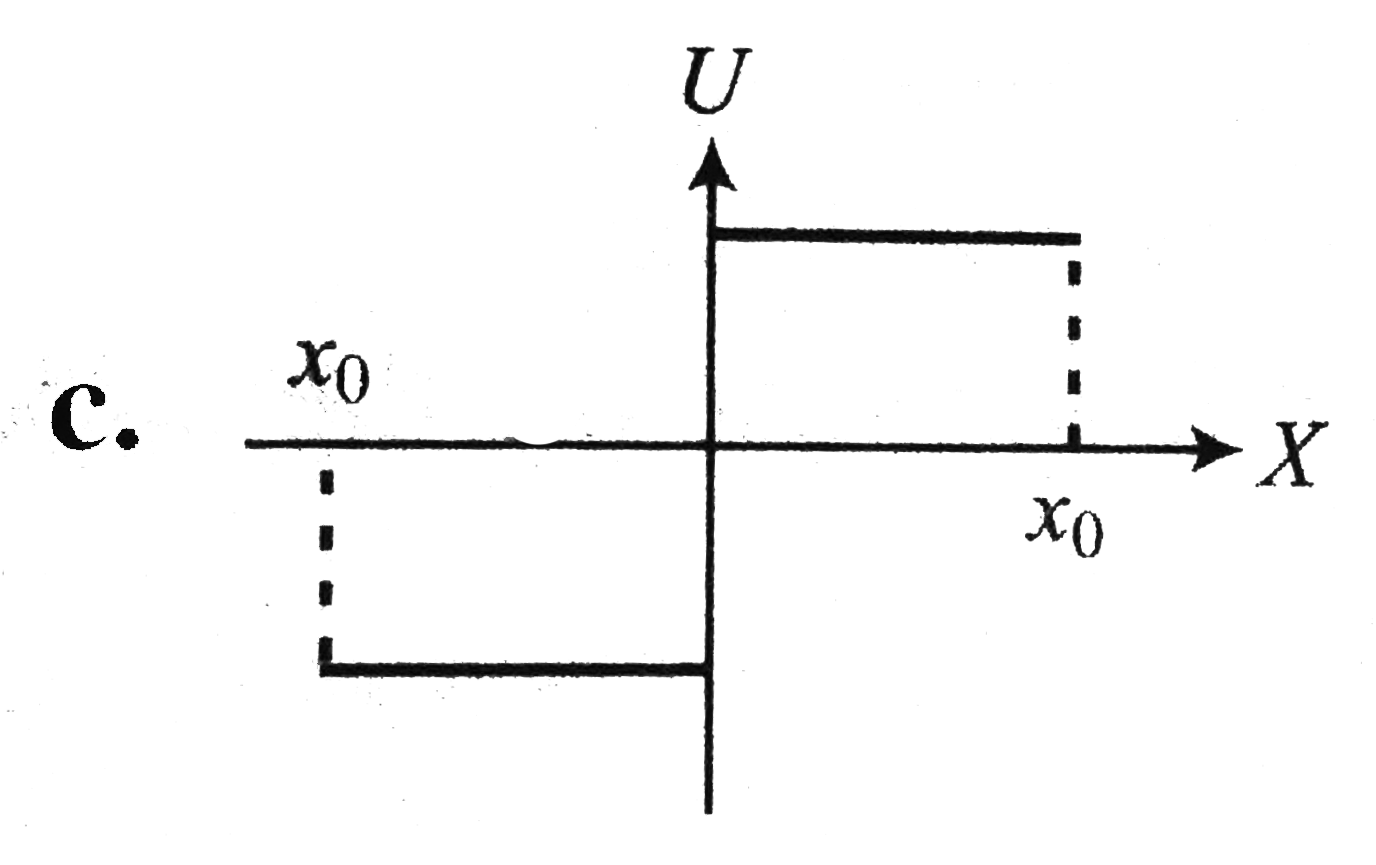 D
D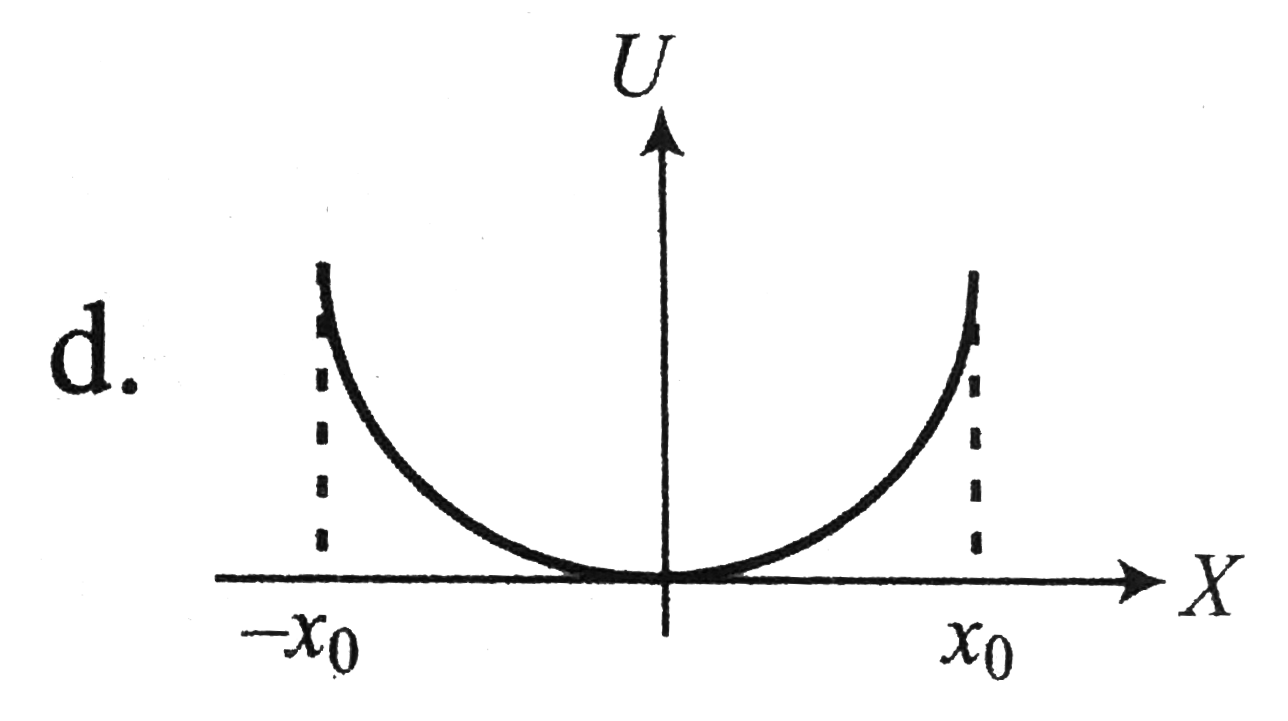
Figure given below shows the variation of potential energy function U(x), corresponding to one dimensional force field. The point on the graph representing the position of most stable equilibrium is :
(##NAR_NEET_PHY_XI_P2_C06_E09_112_Q01.png" width="80%">AABBCCDDFigure given below shows the variation of potential energy function U(x), corresponding to a particle lying in a one dimensional force field. The force acting on the particle at x = 2 m is:
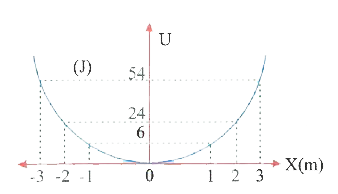 A−12NB−24NC−16ND−8N
A−12NB−24NC−16ND−8N
The relation between conservative force and potential energy U is given by :–
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region

View SolutionAn electric dipole in a uniform electric field has potential energy U. The magnitude of the torque acting on the dipole due to the field is τ.
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region

View SolutionThe given plot shows the variation of U, the potential energy of interaction between two particles with the distance separating them r,

View Solution
