Seven girls $G_{1}, G_{2}, G_{3}$ , …, $G_{7}$ are such that their ages are in order $G_{1} < G_{2} < G_{3} < \dots < G_{7}$ . Five girls are selected at random and arranged in increasing order of their ages. The probability that $G_{5}$ and $G_{7}$ are not consecutive is

A

$\frac{20}{21}$

B

$\frac{19}{21}$

C

$\frac{17}{21}$

D

$\frac{13}{21}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Required probability = 1 - P ( $G_{5}$ and $G_{7}$ are consecutive)
$= 1 - \frac{.^{4} C_{3}}{.^{7} C_{5}} = \frac{17}{21}$

|

Updated on:21/07/2023

Class 12 MATHS PROBABILITY

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
$G_{1}$ and $G_{2}$ genetically identical because

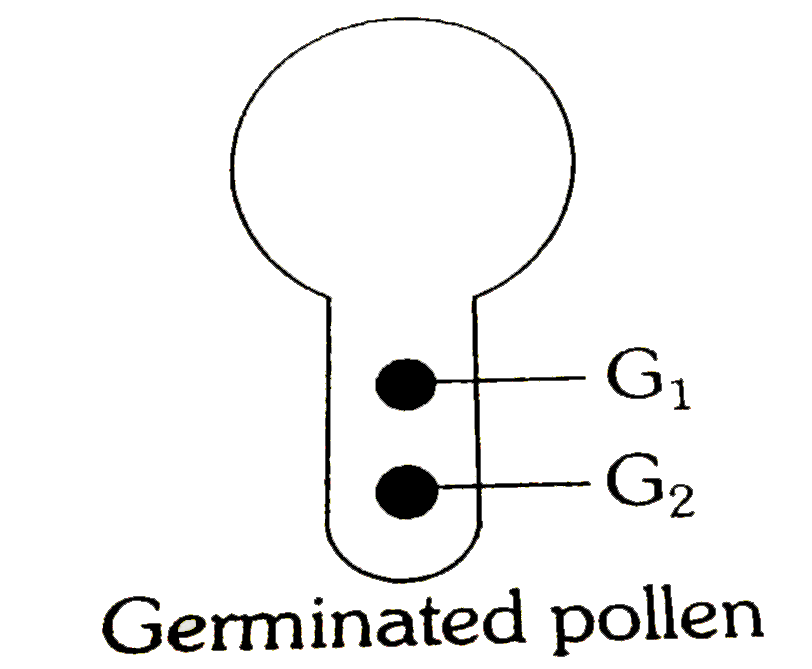AThey are products of meiosis I
BThey are products of amitosis
CThey are products of meiosis
DThey are products of mitosis
Question 2 - Select One
$G_{1}, S and G_{2}$ are stages of
AInterphase
BProphase
CMetaphase
DAnaphase
Question 3 - Select One
If $A_{1}, A_{2}$ be two A.M.'s and $G_{1}, G_{2}$ be two G.M.,s between a and b, then $\frac{A_{1} + A_{2}}{G_{1} G_{2}}$ is equal to
A $\frac{a + b}{2 a b}$
B $\frac{2 a b}{a + b}$
C $\frac{a + b}{a b}$
D $\frac{a + b}{\sqrt{a b}}$

CENGAGE-PROBABILITY I -Exercise (Single)

Home
Ask Doubt
Profile