n whole numbers are randomly chosen and multiplied. Now, match the following lists.
List I List IIa. The probability that the last digit is 1, 3, 7, or 9 isp. 8n−4n10nb. The probability that the last digit is 2, 4, 6, 8 is q. 5n−4n10nc. The probability that the last digit is 5 isr. 4n10nd. The probability that the last digit is zero iss. 10n−8n−5n+4n10n
abcdqssr
abcdrqqp
abcdqpps
abcdqspr
The correct Answer is:A, B, C, D
a. The required event will occur if last digit in all the chosen numbers is 1, 3, 7, or 9. Therefore, the required probability is (4/10)n.
b. The required probability is equal to the probability that the last digit is 2, 4, 6, 8 and is given by
P(last digit is 1, 2, 3, 4, 6, 7, 8, 9)
-P (last digit is 1, 3, 7, 9) = 8n−4n10n
c. P(1, 3, 5, 7, 9) - P(1, 3, 7, 9) = 5n−4n10n
d. The required probability is
P(0,5)−P(5)=(10n−8n)−(5n−4n)10n
P(0,5)−P(5)=(10n−8n)−(5n−4n)10n
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Numerical)
7 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - JEE Main Previous Year
4 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Comprehension)
14 Videos
- PROBABILITY AND STATISTICSBOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank
37 Videos
- PROBABILITY IIBOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - NUMARICAL VALUE TYPE
2 Videos
Similar Questions
n whole are randomly chosen and multiplied
Column I, Column II
The probability that the last digit is 1,3,7, or 9 is, p. 8n−4n10n
The probability that the last digit is 2,4,6, or 8 is, q. 5n−4n10n
The probability that the last digit is 5 is, r. 4n10n
The probability that the last digit is zero is, s. 10n−8n−5n+4n10n
View SolutionMatch the following itmes of List -I and List - II

View Solution
Knowledge Check
Match the following List -I and List - II
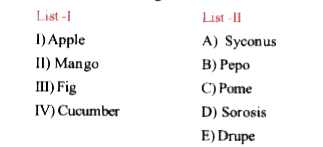 AI-E,II-C,IN-B.IV-DBI-A,II-E,III-B, IV-DCI-A,II-B,III-C, IV-DDI-C, II-E,III-A.IV-B
AI-E,II-C,IN-B.IV-DBI-A,II-E,III-B, IV-DCI-A,II-B,III-C, IV-DDI-C, II-E,III-A.IV-BMatch the following List-I with List-II.
 APQRS2413BPQRS3142CPQRS1324DPQRS2431
APQRS2413BPQRS3142CPQRS1324DPQRS2431Match of the following List-I and List-II
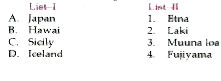 AA-1, B-2, C-3, D-4BA-4, B-3, C-2, D-1CA-3, B-2, C-1, D-2DA-3, B-4, C-1, D-2
AA-1, B-2, C-3, D-4BA-4, B-3, C-2, D-1CA-3, B-2, C-1, D-2DA-3, B-4, C-1, D-2
Match the following itmes of List -I and List - II

View SolutionMatch the following items of List -I and List - II

View SolutionMatch the following items of List -I and List - II

View SolutionMatch the following items of List -I and List - II

View SolutionMatch the following items of List -I and List - II

View Solution
