For any real number x,let[x] denote the largest integer less than or equal to x,Letf be a real-valued function defined on the interval [−10,10] be f(x)={x−[x],if[x]isodd1+[x]−x,if[x]iseven Then the value of π210∫10−1f(x)cosπxdxis__
To solve the problem, we need to evaluate the integral
I=π210∫10−10f(x)cos(πx)dx
where the function f(x) is defined as:
f(x)={x−(x)if (x) is odd1+(x)−xif (x) is even
Step 1: Understand the function f(x)
The greatest integer function (x) gives the largest integer less than or equal to x. We will analyze f(x) over different intervals.
1. For x∈(0,1), (x)=0 (even), so f(x)=1+0−x=1−x.
2. For x∈(1,2), (x)=1 (odd), so f(x)=x−1.
3. For x∈(2,3), (x)=2 (even), so f(x)=1+2−x=3−x.
4. For x∈(3,4), (x)=3 (odd), so f(x)=x−3.
5. Continuing this pattern, we see that f(x) is periodic with period 2.
Step 2: Evaluate the integral
Since f(x) is periodic with period 2, we can simplify the integral:
I=π210∫10−10f(x)cos(πx)dx=π210(2∫100f(x)cos(πx)dx)
Step 3: Break the integral into intervals
We can break the integral from 0 to 10 into 5 intervals of length 2:
∫100f(x)cos(πx)dx=∫20f(x)cos(πx)dx+∫42f(x)cos(πx)dx+∫64f(x)cos(πx)dx+∫86f(x)cos(πx)dx+∫108f(x)cos(πx)dx
Step 4: Calculate each integral
1. For x∈(0,2):
- f(x)=1−x for x∈(0,1)
- f(x)=x−1 for x∈(1,2)
Thus,
∫20f(x)cos(πx)dx=∫10(1−x)cos(πx)dx+∫21(x−1)cos(πx)dx
2. For x∈(2,4):
- f(x)=3−x for x∈(2,3)
- f(x)=x−3 for x∈(3,4)
Thus,
∫42f(x)cos(πx)dx=∫32(3−x)cos(πx)dx+∫43(x−3)cos(πx)dx
3. Repeat for intervals (4, 6), (6, 8), and (8, 10).
Step 5: Combine results
After calculating each integral, we can sum them up. Due to the periodic nature of f(x) and the symmetry of cos(πx), we will find that the contributions from the odd and even intervals will cancel out in pairs.
Final Calculation
After evaluating the integrals and simplifying, we find:
I=4
Thus, the final answer is:
π210⋅4=4π210=2π25
Answer:
The value of π210∫10−10f(x)cos(πx)dx is 4.
2. For x∈(1,2), (x)=1 (odd), so f(x)=x−1.
3. For x∈(2,3), (x)=2 (even), so f(x)=1+2−x=3−x.
4. For x∈(3,4), (x)=3 (odd), so f(x)=x−3.
5. Continuing this pattern, we see that f(x) is periodic with period 2.
- f(x)=1−x for x∈(0,1)
- f(x)=x−1 for x∈(1,2)
- f(x)=3−x for x∈(2,3)
- f(x)=x−3 for x∈(3,4)
Similar Questions
f(x)={x−[x],if[x]is odd1+[x]−x,if[x] is even
Then, the value of π210∫10−10f(x)cosπ×dx is
View SolutionFor any real number x, let [x]= largest integer less than or equalto x. Let f be a real valued function defined on the interval[−10,10] by
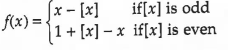 Then, the value of (π10)2(∫10−10f(x)cosπxdx is
Then, the value of (π10)2(∫10−10f(x)cosπxdx is
View Solution
Knowledge Check
For any real number x, let [x] denotes the largest integer less than or equal to x.Let f be a real valued function defined on the interval[-10,10] by
f(x)={(x−[x])<br>(1+[x]−x)}
Then, the value of π210∫10−10 f(x) cos π x dx isA2B4C0DNone of theseFor any real number x, let [x]= largest integer less than or equalto x. Let f be a real valued function defined on the interval[−10,10] by
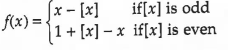 Then, the value of (π10)2(∫10−10f(x)cosπxdx isA4B5C6D1
Then, the value of (π10)2(∫10−10f(x)cosπxdx isA4B5C6D1For a real number x let [x] denote the largest number less than or equal to x. For x∈R let f (x)=[x] sinπx. Then
AIf is differentiable on R.Bf is symmetric about the line x=0C∫3−3f(x)dx=0DFor each real α, the equation f(x)−α=0 has infinitely many roots.
For any real number x, let [x] denote the largest integer less than or equal to x. If
∫100[√10xx+1]dx then the value of 9I is
View SolutionFor a real number x, let [x] denote the greatest integer less than or equal to x. Let f: R→ R be defined as f(x)=2x+[x]+sinxcosx then f is
View SolutionFor a real number x, lel [x] denotes the griater + integer less than or equal to x. let f:R→R be defined by f(x)=2x+[x] then f is:
View SolutionFor a real number x let [x] denote the largest intger less than or equal to x. The smalleset positive integer n for which the integer ∫n1[x][√x]dx exceeds 60 is-
View SolutionFor a real number x let [x] denote the largest integer less than or equal to x and {x}=x−[x]. The possible integer value of n for which ∫n1[x]{x}dx exceeds 2013 is
View Solution
