Assertion: If position vector is given by ˆr=sinhati+costˆj−7tˆk, then magnitude of acceleration |→a|=1
Reason: The angles which the vector →A=A1→i+A3ˆk makes with the co-ordinate
asex are given by cosα=A1A,cosβ=A2A&cosγ=A3A.
If both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.
If both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.
If Assertion is True but the Reason is False.
If both Assertion & Reason are false.
The correct Answer is:B
To solve the given problem, we need to analyze the assertion and the reason provided in the question step by step.
Step 1: Identify the Position Vector
The position vector is given as:
→r=^isint+^jcost−7^k
Step 2: Calculate the Velocity Vector
To find the velocity vector →v, we differentiate the position vector →r with respect to time t:
→v=d→rdt=ddt(^isint+^jcost−7^k)
Calculating the derivatives:
→v=^icost−^jsint+0^k=^icost−^jsint
Step 3: Calculate the Acceleration Vector
Next, we find the acceleration vector →a by differentiating the velocity vector →v with respect to time t:
→a=d→vdt=ddt(^icost−^jsint)
Calculating the derivatives:
→a=−^isint−^jcost
Step 4: Calculate the Magnitude of the Acceleration Vector
Now, we calculate the magnitude of the acceleration vector |→a|:
|→a|=√(−sint)2+(−cost)2=√sin2t+cos2t
Using the Pythagorean identity sin2t+cos2t=1:
|→a|=√1=1
Step 5: Analyze the Assertion
The assertion states that the magnitude of acceleration |→a|=1. From our calculations, we found that this statement is true.
Step 6: Analyze the Reason
The reason provided states that the angles which the vector →A makes with the coordinate axes are given by:
cosα=A1A,cosβ=A2A,cosγ=A3A
This is indeed a correct statement regarding direction cosines of a vector. However, it does not directly explain why the magnitude of acceleration is 1.
Conclusion
Both the assertion and reason are true, but the reason does not correctly explain the assertion. Therefore, the correct conclusion is that the assertion is true and the reason is true but not a correct explanation of the assertion.
Final Answer
The assertion is true, and the reason is true but does not explain the assertion.
---
→r=^isint+^jcost−7^k
→v=d→rdt=ddt(^isint+^jcost−7^k)
Calculating the derivatives:
→v=^icost−^jsint+0^k=^icost−^jsint
→a=d→vdt=ddt(^icost−^jsint)
Calculating the derivatives:
→a=−^isint−^jcost
|→a|=√(−sint)2+(−cost)2=√sin2t+cos2t
Using the Pythagorean identity sin2t+cos2t=1:
|→a|=√1=1
cosα=A1A,cosβ=A2A,cosγ=A3A
This is indeed a correct statement regarding direction cosines of a vector. However, it does not directly explain why the magnitude of acceleration is 1.
Topper's Solved these Questions
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - UNIT & DIMENSIONS
19 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - ERRORS IN MEASURMENTS
20 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-2
80 Videos
- AIIMS 2019BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS
40 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
Similar Questions
Knowledge Check
If α,β,γ are the direction angles of a vector and cosα=1415,cosβ=13, then cosγ=
A±215B±15C±115D±415The direction consines of a vector →A are cosα=45√2,cosβ=1√2 and cosγ=35√2 then the vector →A is
A4ˆi+ˆj+3ˆkB4ˆi+5ˆj+3ˆkC4ˆi−5ˆj−3ˆkDˆi+5ˆj−ˆkA point on the periphery of a rotating disc has its acceleration vector making angle of 30∘ with the velocity . The ratio (ac/at(ac "is centripetal acceleration and a1 is tangential acceleration ") equals
Asin30∘Bcos30∘Ctan30∘DNone
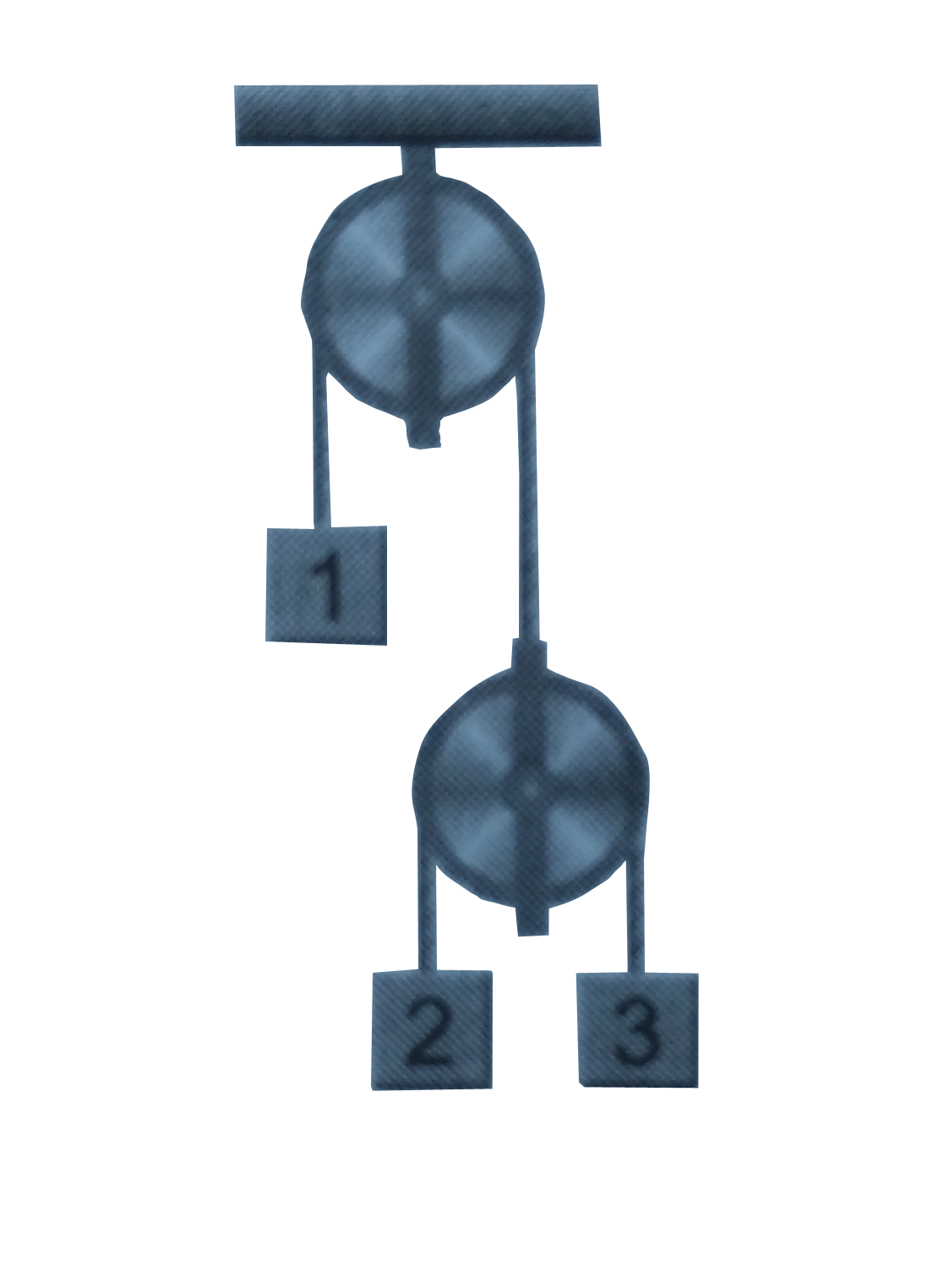
Make the constraint relation between a1,a2 and a3
View SolutionIf a1anda2 aare two non- collineaar unit vectors and if |a1+a2|=√3, ,then value of (a1−a2).(2a1−a2) is
View SolutionLet →a,→b,→c be vectors of equal magnitude such that the angle between →aand→b is α,→band→c is βand→cand→a is γ .then minimum value of cosα+cosβ+cosγ is
View SolutionIf →a1and→a2are two non-collinear unit vectors and if ∣∣→a1+→a2∣∣=√3, then the value of (→a1−→a2).(2→a1+→a2) is :
View SolutionTwo vectors →A1and→A2 each of magnitude A are inclinded to each other such that their resultant is equal to √3A. What is the magnitude of the resultant of →A1and−→A2 is
View Solution
