Assertion : The unit vectors ˆi,ˆjandˆk have of distance and dimensions [MoL1To].
Reason : The product of a scalar and a vector of a new scalar.
If both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.
If both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.
If Assertion is True but the Reason is False.
If both Assertion & Reason are false.
Step by step video & image solution for Assertion : The unit vectors hati, hatj and hatk have of distance and dimensions [M^(o)L^(1)T^(o)]. Reason : The product of a scalar and a vector of a new scalar. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - UNIT & DIMENSIONS
19 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - ERRORS IN MEASURMENTS
20 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - EXERCISE-2
80 Videos
- AIIMS 2019BOOK - ALLENCHAPTER - AIIMS 2019EXERCISE - PHYSICS
40 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
Similar Questions
Knowledge Check
A unit vector perpendicular to both ˆi+ˆjandˆj+ˆk is
Aˆi−ˆj+ˆkBˆi+ˆj+ˆkCˆi+ˆj+ˆk√3Dˆi−ˆj+ˆk√3The scalar triple product of the vectors 2ˆi,3ˆjand−5ˆk is
A0B10C−15D−30Assertion : A vector can have zero magnitude if one of its rectangular components is not zero.
Reason : Scalar product of two vectors cannot be a negative quantity.A[ε0]=[M−1L−3T2I]B[ε0]=[M−1L−3T4I2]C[μ0]=[MLT−2I−2]D[μ0]=[ML2T−1I]
Define the term pressure.Is it a scalar or a vector? Give its units and dimensions.
View SolutionGiven names of a scalar quantity and a vector quantity which have same dimensions.
View SolutionAssertion: The dot product of one vector with another vector may be scalar or a vector.
Reason: If the product of two vectors is a vector quantity, then product is called a dot product.
View SolutionThe unit vectors ˆi,ˆj and ˆk are as shown below. What will be the magnetic field at O in the following figure
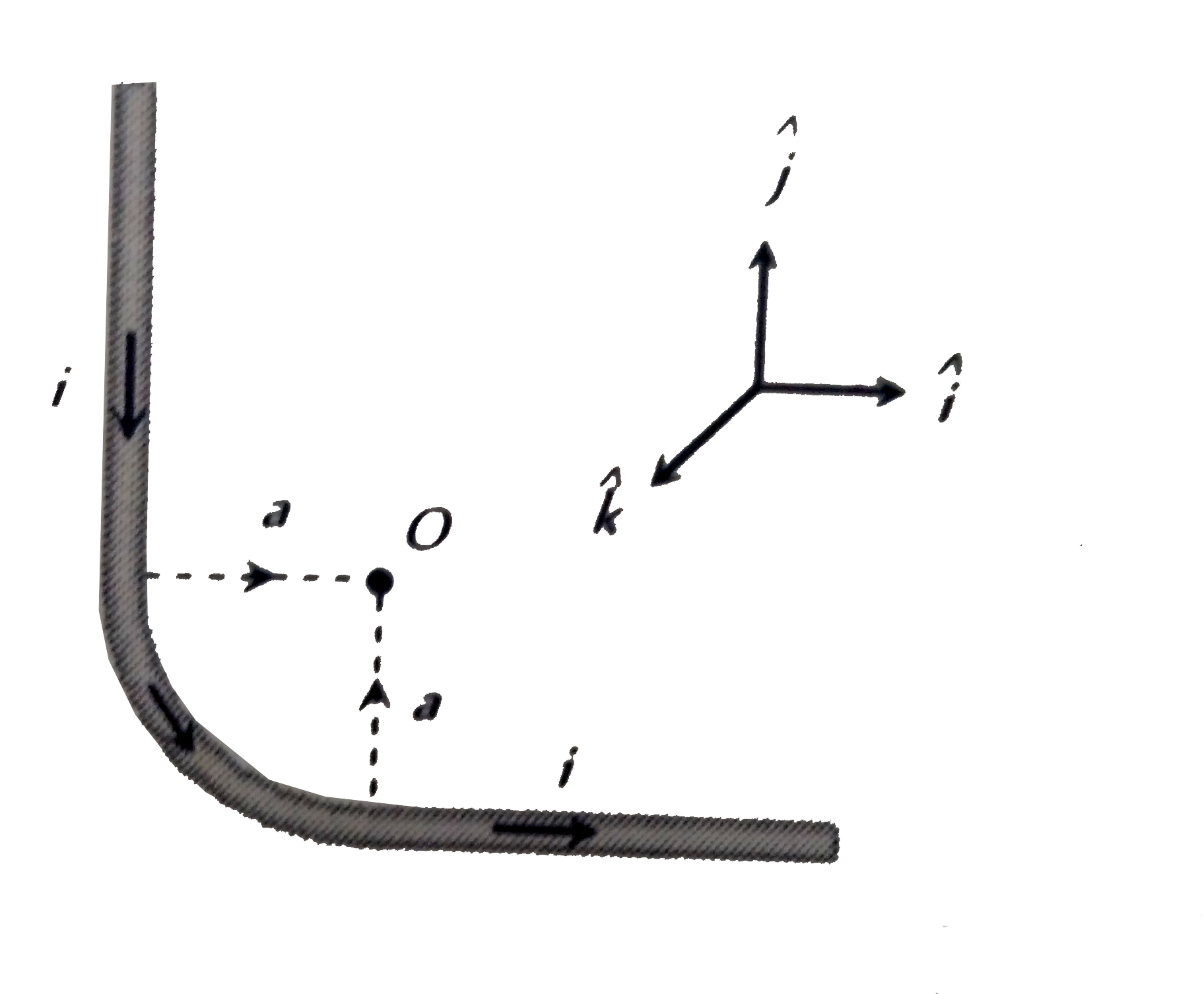
View SolutionThe scalar product of two vectors A=2ˆi+2ˆj−ˆkandB=−ˆj+ˆk ,is given by
View Solution
