A projectile is projected from ground with initial velocity →u=u0ˆi+v0ˆj. If acceleration due to gragvity (g) is along the negative y-direction then find maximum displacement in x-direction.
u202g
2u0v0g
v202g
4u0v0g
The correct Answer is:B
To solve the problem of finding the maximum displacement in the x-direction for a projectile projected from the ground with an initial velocity →u=u0^i+v0^j, we can follow these steps:
Step 1: Understand the motion components
The initial velocity has two components:
- Horizontal component: ux=u0
- Vertical component: uy=v0
Step 2: Determine the time of flight
The time of flight T can be determined by analyzing the vertical motion. The vertical motion is influenced by gravity, which acts downwards. The equation of motion in the vertical direction is given by:
y=uyt−12gt2
At the maximum height, the vertical displacement y will be 0 (since it returns to the ground). Therefore, we set the equation to zero:
0=v0t−12gt2
Factoring out t:
t(v0−12gt)=0
This gives us two solutions:
1. t=0 (at the time of projection)
2. t=2v0g (time of flight)
Step 3: Calculate the maximum displacement in the x-direction
The horizontal displacement x can be calculated using the horizontal component of the velocity and the time of flight:
x=ux⋅T
Substituting the values we have:
x=u0⋅2v0g
Final Expression
Thus, the maximum displacement in the x-direction is:
Maximum Displacement in x-direction=2u0v0g
The initial velocity has two components:
- Horizontal component: ux=u0
- Vertical component: uy=v0
The time of flight T can be determined by analyzing the vertical motion. The vertical motion is influenced by gravity, which acts downwards. The equation of motion in the vertical direction is given by:
1. t=0 (at the time of projection)
2. t=2v0g (time of flight)
The horizontal displacement x can be calculated using the horizontal component of the velocity and the time of flight:
Thus, the maximum displacement in the x-direction is:
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-2170videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-341videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE28videos
MOTION IN A PALNE
- BOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)48videos
KINEMATICS-2D
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
Similar Questions
A projectile is projected from ground with an initial velocity (5ˆi+10ˆj)m/s If the range of projectile is R m, time of flight is Ts and maximum height attained above ground is Hm, find the numerical value of R×HT. [Take g=10m/s2]
View SolutionA region has a uniform magnetic field B along positive x direction and a uniform electric field E in negative x direction. A positively charged particle is projected from origin with a velocity −−→V=V0ˆi+V0ˆj . After some time the velocity of the particle was observed to beV0ˆJ while its x co-ordinate was positive. Write all possible values of EB
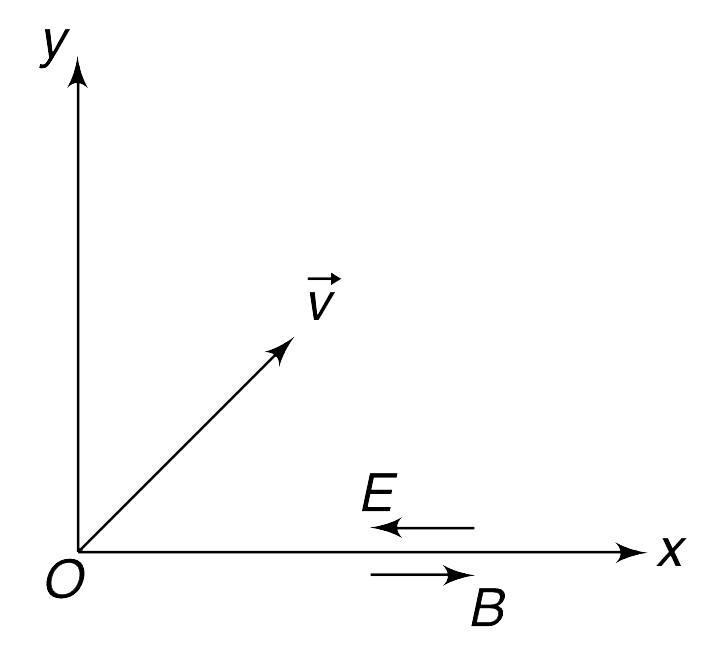 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A particle is projected from ground with velocity 3ˆi+4ˆi m/s. Find range of the projectile :-
A1.2mB3.6mC2.4mD10m - Question 2 - Select One
A projectile is thrown with an initial velocity (vxˆi+vyˆj)ms−1. If the range of the projectile is double the maximum height , then vyvx is
A1B2C3D4 - Question 3 - Select One
A particle at origin (0,0) moving with initial velocity u=5msˆj and acceleration 10ˆi+4ˆj. After t time it reaches at position (20,y) then find t & y
At = 2, y = 18Bt = 4, y = 16Ct = 6, y = 12Dt =8, y =10
A projectile is projected with velocity u making angle θ with horizontal direction, find : time of flight.
View SolutionA projectile is projected with velocity u making angle θ with horizontal direction, find : horizontal range.
View SolutionA body is prodected with initial velocity(5ˆi+12ˆi) m//s from origin . Gravity acts in negative y direction. The horizontal rang is (Take g = 10 m/s2)
View SolutionA body is projected from the ground with a velocity v=(3ˆi+10ˆj)ms−1. The maximum height attained and the range of the body respectively are (given g=10ms−2)
View SolutionA projectile is thrown with a velocity →v0=3ˆi+4ˆjms−1 where ˆIandˆj are the unit vectors along the horizontal and vertical directions respectively. The speed of the projectile at the highest point of its motion in ms−1 is
View Solution

