In the above, the change in speed is:-
A
ucosθ
B
u
C
usinθ
D
(ucosθ−u)
Text Solution
The correct Answer is:D
Δ→v=→vtop−→v1
(ucosθ)ˆi−[(ucosθ)ˆi+(usinθ)ˆj]=−(usinθ)ˆj
|Δ→v|=usinθ
change in speed =(ucosθ)−v
|
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-3
41 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-1
99 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
48 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
A particle moving with a speed v changes direction by an angle θ, without change in speed.
View SolutionAn altimeter is an aneroid barometer which makes use of the change in atmospheric pressure with the change in height above the sea level (altitude).
How does the atmospheric pressure change with increase in height above the sea level?
View Solution
Knowledge Check
In the above problem, the change in velocity cfter covering an angle of 90∘ will be
Azero km//hB300km/hC600km/hD300√2km/hA particle moving with a speed v changes direction by an angle θ, without change in speed.
AThe change in the magnitude of its velocity is zeroBThe change in the magnitude of its velocity is 2vsin(θ/2)CThe magnitude of the change in its velocity is 2vsin(θ/2)DThe magnitude of the change in its velocity is v(1−cosθ)Aparticle moves with a speed v changes direction by an angle θ, without change in speed.
Athe change in the magnitude in velocity is zeroBthe change in the magnitude fo its velocity is 2vsinθ/2Cthe magnitude of change in velcoity is 2vsinθ/2Dthe magnitude of change in velocity is v(1−cosθ)
In the above question, change in internal energy of gas is
View SolutionIn the above question, change in internal energy of gas is
View SolutionIn the above question, escape speed from the centre of earth is :
View SolutionIn the above question, the speed of the particle at origin will be:
View Solution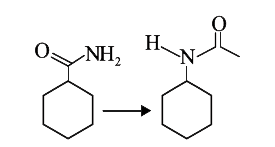
The correct route for the above change is :
View Solution
