A cylindrical vessel filled with water upto a height of 2m stands on horizontal plane. The side wall of the vessel has a pugged circular hole touching the bottom. If the minimum diameter of the hole so that the vessel begins to move on the floor if the plug is removed is x10√π meter then x will be (if the coefficient of frication between the bottom of the vessel and the plane is 0.4 and total mass of water plus vessel is 100kg.)
√2μMπρH
√μM2πρH
√μMρH
none
The correct Answer is:A
Force on vessel = rate of change of linear momentum imparted to flow water through hole.
Force on vessel = mv (where m is coming out per second)
(v = volume coming out per second)
F=mv F=ρVv⇒F=ρ.av.v⇒F=ρav2
μMg≤ρ.πd24v2[put v=√2gh] ⇒μMg≤ρπd24.2gh⇒dmin=√2μMπρH
Topper's Solved these Questions
Similar Questions
A cylindrical vessel, open at the top, has a radius 10 cm and height 14 cm. Find the total surface area of the vessel. (Take pi = 3.14)
View SolutionA cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View Solution
Knowledge Check
- Question 1 - Select One
A cylindrical vessel filled with water upto a height of 2m stands on horizontal plane. The side wall of the vessel has a pugged circular hole touching the bottom. If the minimum diameter of the hole so that the vessel begins to move on the floor if the plug is removed is x10√π meter then x will be (if the coefficient of frication between the bottom of the vessel and the plane is 0.4 and total mass of water plus vessel is 100kg.)
A√2μMπρHB√μM2πρHC√μMρHDnone - Question 2 - Select One
A cylinderical vessel is filled with water up to height H. A hole is bored in the wall at a depth h from the free surface of water. For maximum range h is equal to
AH/4BH/2C3H/4DH - Question 3 - Select One
A cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x
 Ax is equal if hole is at depth y or H-yBx is maximum for y=H/2CBoth (a ) and (b) are correctDBoth (d) and (d) are wrong
Ax is equal if hole is at depth y or H-yBx is maximum for y=H/2CBoth (a ) and (b) are correctDBoth (d) and (d) are wrong
A cylindrical vessel filled with water to a hight H. A vessel has two small holes in the side, from which water iins rushing out horizontal and the two steams stike the ground at the same poin, if the lower hole Q Q is h height above the ground, then the height of hole P above the ground will be
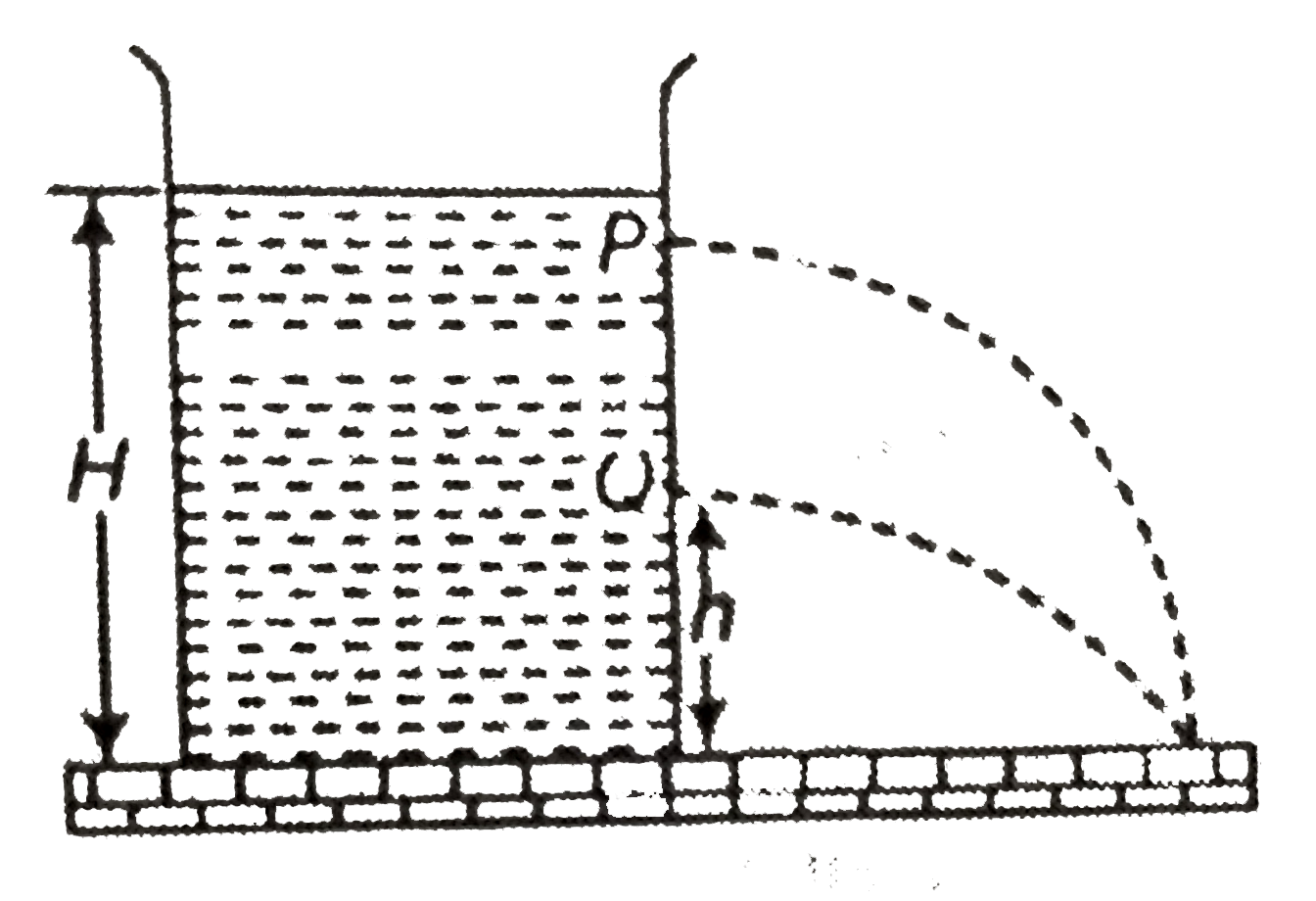 View Solution
View SolutionA closed vessel is half filled with water. There is a hole near the top of vessel and air is pumped out from this hole.
View SolutionA large cylindrical vessel contains water to a height of 10 m. If is found that the thrust acting on the curved surface is equal to that at the bottom. If atmospheric pressure can support a water column of 10 m. the radius of the vessel is
View SolutionA cylindrical vessel of radius R and height H and open at the top is completely filled with y . A small circular hole of radius r is made near the bottom of vessel . The time taken for 25 % of water to flow out is
View SolutionIn a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
View Solution

