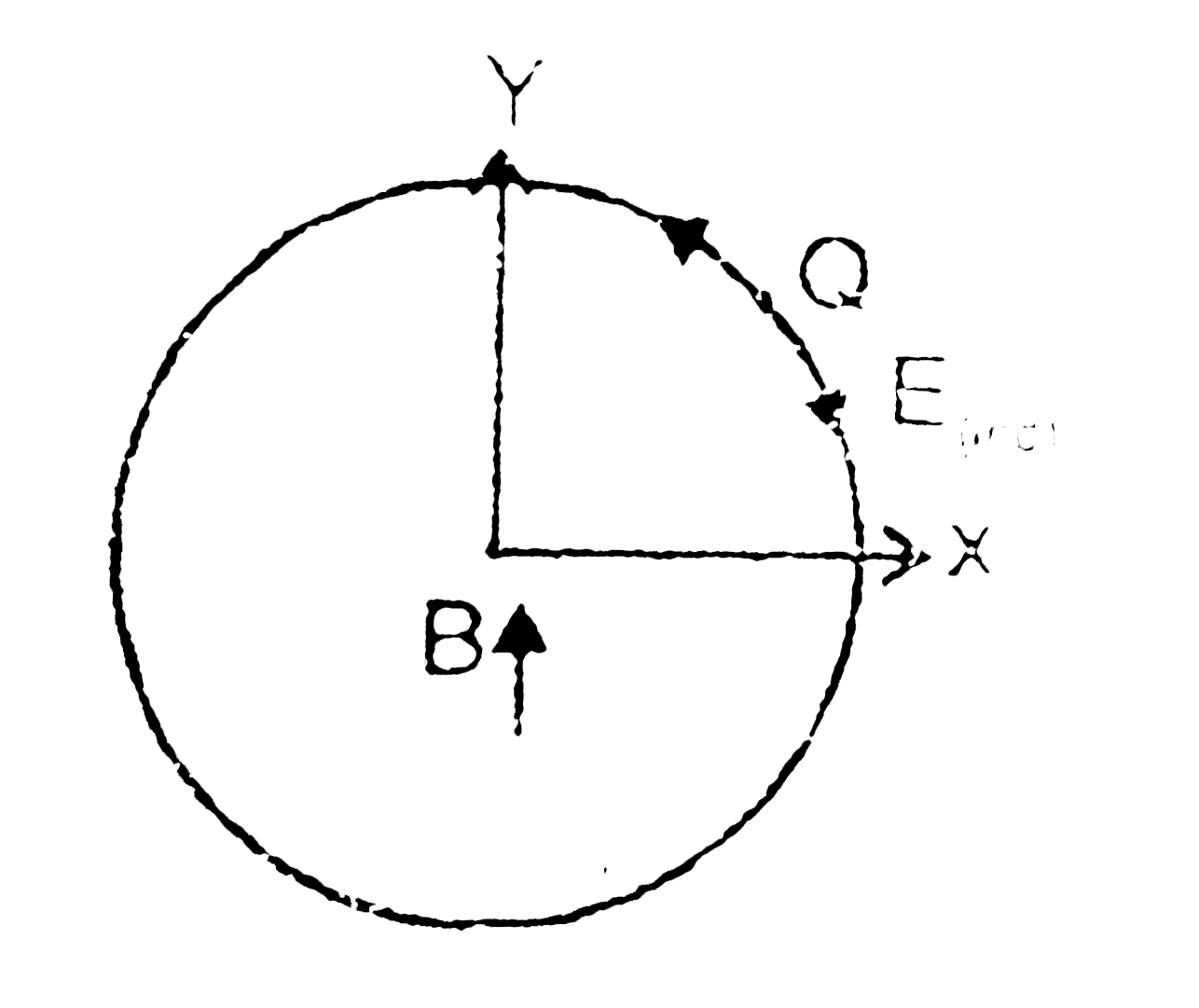
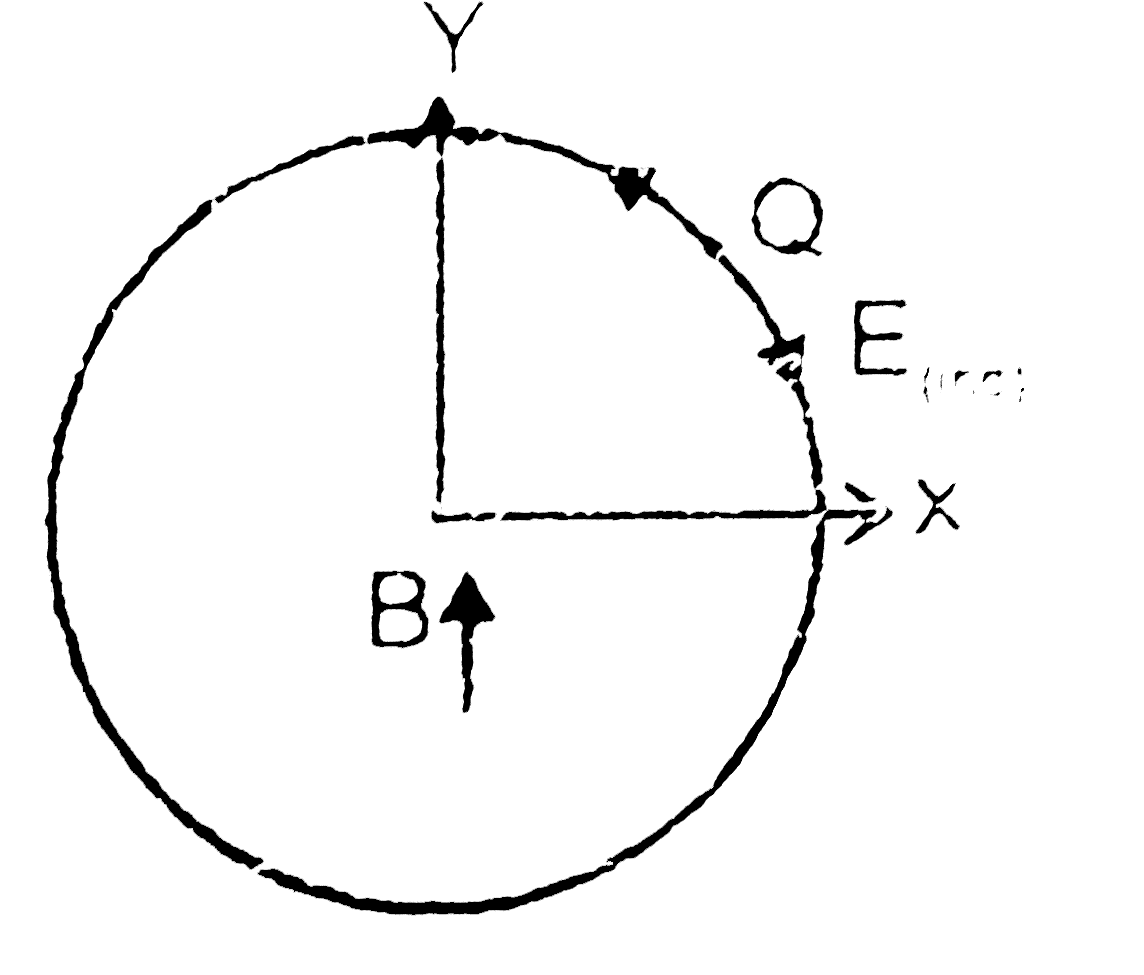
A point charges Q is moving in a circular orbit of radius R in the x-y plane with an angular velocity $ω$ . This can be considered as equivalent to a loop carrying a steady current $\frac{Q ω}{2 π}$ . S uniform magnetic field along the positive z-axis is now switched on, which increases at a constant rate from 0 to B in one second. Assume that the radius of hte orbit remains constant. The application of hte magnetic field induces an emf in the orbit. The induced emf is defined as the work done by an induced electric field in moving a unit positive charge around a closed loop. It si known that, for an orbiting charge, the magnetic dipole moment is proportional to the angular momentum with a porportionality constant $λ$ .
The charge in the magnetic dipole moment associated with the orbit. at the end of the time interval of hte magnetic field charge, is

$- γ B Q R^{2}$

$- γ \frac{B Q R^{2}}{2}$

$γ \frac{B Q R^{2}}{2}$

$γ B Q R^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Megnetic dipole moment $M = γ J$
$Δ M = γ Δ J$ …(i)
$\frac{Δ J}{Δ t} = - Q \frac{d B}{d t} . \frac{R}{2} R . \Rightarrow Δ J = - \frac{Q B}{2} R^{2} \Rightarrow so Δ M = \frac{γ Q B R^{2}}{2}$
Alternate
$\frac{M}{L} = \frac{Q}{2 m}$
$M = \frac{Q ω}{2 π} π R^{2} = \frac{Q ω R^{2}}{2}$ .
induced electric field is opposite to the $ω$ so the charge is retarded.
$ω' = ω - α t$
$ω' = ω - \frac{Q B}{2} 1, (a_{1} = Q E / m), (α = \frac{Q E}{m R} = \frac{Q}{R} \times \frac{B R}{2 m} = \frac{Q B}{2 m})$
$M_{f} = \frac{Q ω' R^{2}}{2} = Q (ω - \frac{Q B}{2 m}) \frac{R^{2}}{2}$
$Δ m = M_{f} - M_{i} = \frac{Q ω R^{2}}{2} - \frac{Q^{2} B R^{2}}{4 m} - \frac{Q ω R^{2}}{2} = - γ \frac{B Q R^{2}}{2}$
Alternate
$\frac{M}{L} = \frac{Q}{2 m}$
$M = \frac{Q ω}{2 π} π R^{2} = \frac{Q ω R^{2}}{2}$ .
$ω' = ω - α t$
$ω' = ω - \frac{Q B}{2} 1, (a_{1} = Q E / m), (α = \frac{Q E}{m R} = \frac{Q}{R} \times \frac{B R}{2 m} = \frac{Q B}{2 m})$
$M_{f} = \frac{Q ω' R^{2}}{2} = Q (ω - \frac{Q B}{2 m}) \frac{R^{2}}{2}$
$Δ m = M_{f} - M_{i} = \frac{Q ω R^{2}}{2} - \frac{Q^{2} B R^{2}}{4 m} - \frac{Q ω R^{2}}{2} = - γ \frac{B Q R^{2}}{2}$

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Knowledge Check

A point charge Q is moving in a circular orbit of radius R in the x-y plane with an angular velocity $ω$ . This can be considered as equivalent to a loop carrying a steady current $Q ω / 2 π$ . A uniform magnetic field along the positive z-axis is now switched on, which increases at a constant rate from 0 to B in one second. Assume that the radius of the orbit remains constant. The application of the magnetic field induces an emf in the orbit. The induced emf is defined as the work done by an induced electric field in moving a unit positive charge around a closed loop. It is known that , for an orbiting charge, the magnetic dipole moment is proportional to the angular momentum with a proportionally constant $γ$
The change in the magnetic dipole moment associated with the orbit, at the end of the time interval of the magnetic field change is :
A $- γ B Q R^{2}$
B $- γ \frac{B Q R^{2}}{2}$
C $γ \frac{B Q R^{2}}{2}$
D $γ B Q R^{2}$
A point charges Q is moving in a circular orbit of radius R in the x-y plane with an angular velocity $ω$ . This can be considered as equivalent to a loop carrying a steady current $\frac{Q ω}{2 π}$ . S uniform magnetic field along the positive z-axis is now switched on, which increases at a constant rate from 0 to B in one second. Assume that the radius of hte orbit remains constant. The application of hte magnetic field induces an emf in the orbit. The induced emf is defined as the work done by an induced electric field in moving a unit positive charge around a closed loop. It si known that, for an orbiting charge, the magnetic dipole moment is proportional to the angular momentum with a porportionality constant $λ$ .
The charge in the magnetic dipole moment associated with the orbit. at the end of the time interval of hte magnetic field charge, is
A $\frac{B R}{4}$
B $\frac{B R}{2}$
CBR
D2BR
A particle moving along a circule path of radius 'r' with uniform angular velocity $ω$ . Its angular acceleration is
A $r ω^{2}$
B $r / ω$
Czero
D $ω / r$

RESONANCE-ELECTROMAGNETIC INDUCTION-Exercis-3 PART 1

Home
Ask Doubt
Profile

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

A particle moving along a circule path of radius 'r' with uniform angular velocity ω. Its angular acceleration is

RESONANCE-ELECTROMAGNETIC INDUCTION-Exercis-3 PART 1

A particle moving along a circule path of radius 'r' with uniform angular velocity $ω$ . Its angular acceleration is