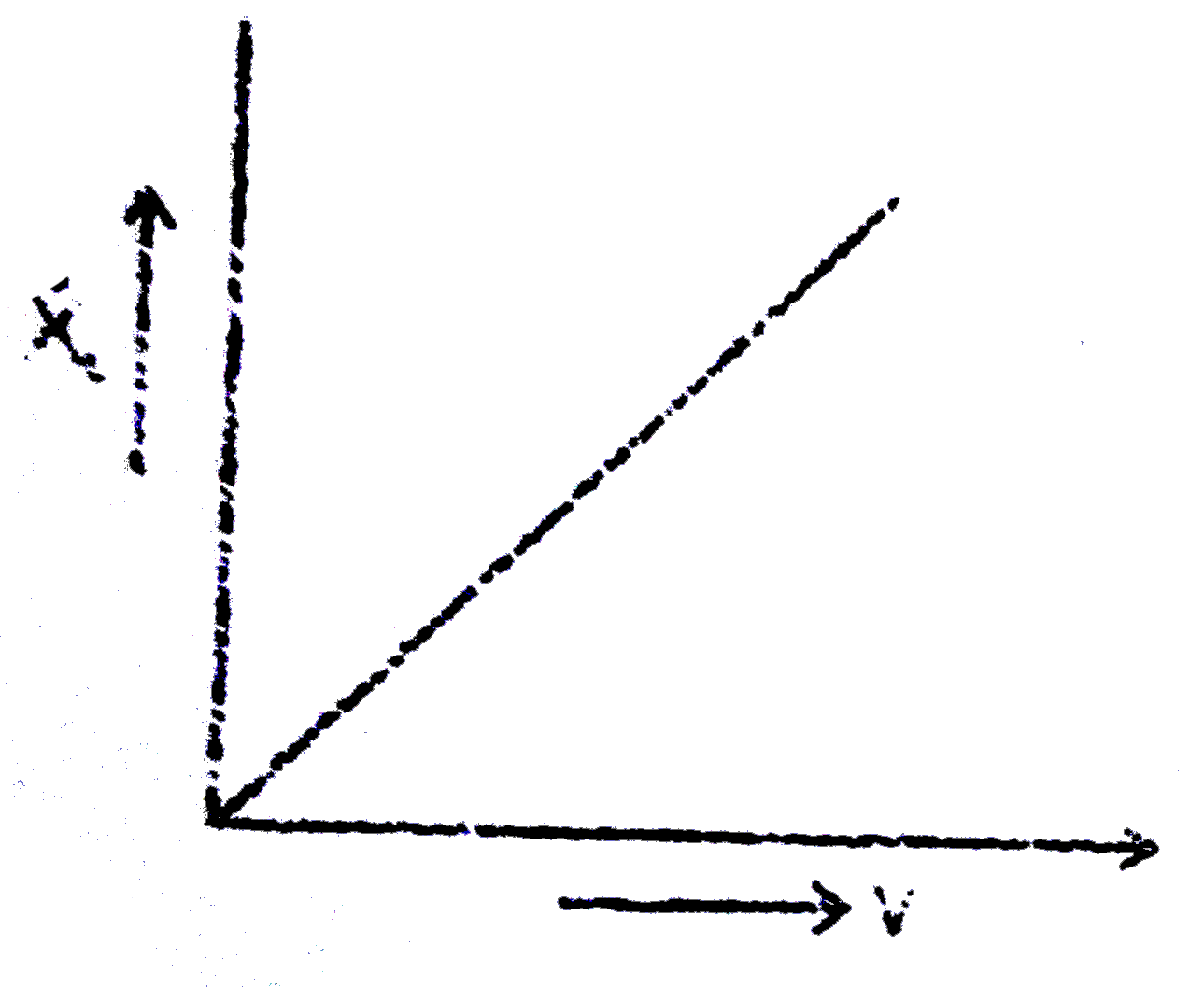
Explain the term 'inductive reactance'.Show graphically the variation of inductive reactance with frequency of the applied alternating voltage.
An $a . c .$ voltage $E = E_{0} sin ω t$ is applied across a pure inductor $L$ .Show mathematically that the current flowing through it lags behind the applied voltage by a phase angle of $π / 2$ .

Video Solution

Text Solution

Verified by Experts

Inductive reactance :The effective resistance offered by inductance $L$ is called inductive reactance.It is denoted by $X_{L}$ .it $S I$ unit is $o h m$ .The graph between frequency $(v)$ and $X_{L}$ is shown in fig.
$A . C .$ Source containing an inductor: Let a source of alternating $e . m . f$ $E = E_{0} sin ω t$ be connected to an inductor of inductance $L$ only.
If $i$ be the current through the circuit, then
instanteous induced $e . m . f$ produced $V = L \frac{d i}{d t}$
$d i = \frac{V}{L} d t$
$d i = \frac{V_{m}}{L} sin ω t d t, [∵ V = V_{m} sin ω t]$
Integrating both sides, we get
$\int d i = \frac{V_{m}}{L} \int sin ω t d t$
$i = \frac{V_{m}}{L} (\frac{- cos ω t}{ω}) = \frac{- V_{m}}{ω L} cos ω t$
$i = \frac{- V_{m}}{ω L} sin (\frac{π}{2} - ω t)$
$= \frac{- V_{m}}{ω L} sin (ω t - \frac{π}{2})$
$i = i_{m} sin (ω t - \frac{π}{2})$ ...(i)
where $i = \frac{V_{m}}{ω L}$ is the amplitude of the current.The quanity $ω L$ is called the inductive reactance and is denoted by $X_{L}$ i.e., $X_{L} ω L$
The equation $(i)$ shows that the current logs the voltage by $\frac{π}{2}$
(or $e . m . f$ lends the current by a phase angle $\frac{π}{2}$ )
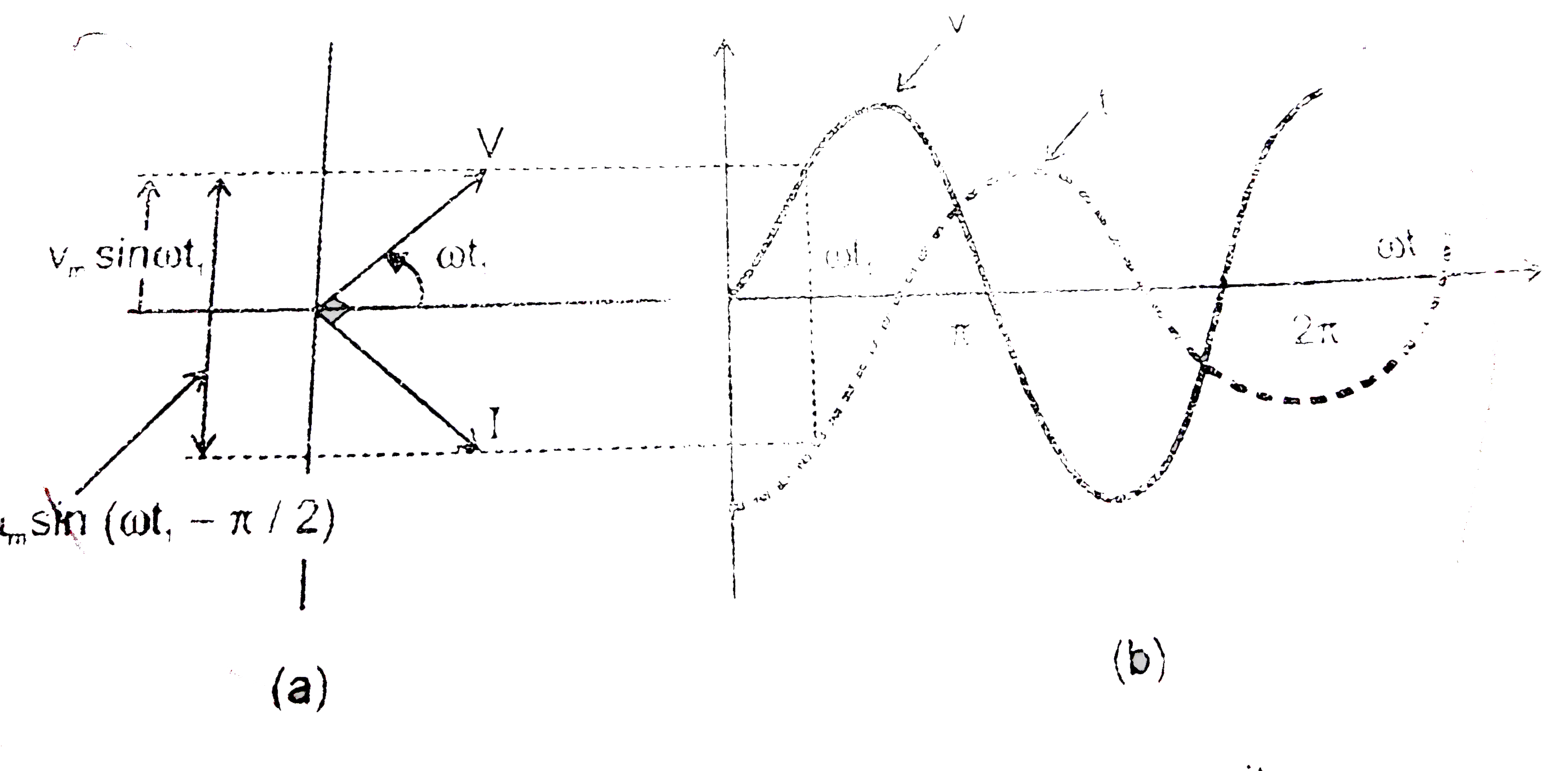
The phasor diagram for the circuit between $\to V$ and $\to i$ at any istant $t$ is shown in Fig. (a)and the graph of $V$ and $i$ versus $ω t$ is shown in Fig. (b)

Updated on:21/07/2023

An alternating voltage $E = E_{0} sin ω t$ , is applied across a coil of inductor L. The current flowing through the circuit at any instant is
A $\frac{E_{0}}{ω L} sin (ω t + π / 2)$
B $\frac{E_{0}}{ω L} sin (ω t - π / 2)$
C $E_{0} ω L sin (ω t - π / 2)$
D $E_{0} ω L sin (ω t + π / 2)$
A small signal voltage $V (t) = V_{0} sin ω t$ is applied across an ideal capacitor $C$ :
ACurrent l(t) leads voltage V(t) by $180^{\circ}$
BCurrent l(t) lags voltage V(t) by $90^{\circ}$
COver a full cycle the capacitor C does not consume any energy from the voltage source
DCurrent l(t) is in phase with voltage V(t)
A small signal voltage $V (t) = V_{0} sin ω t$ is applied across an ideal capacitor $C$ :
ACurrent $I (t)$ , lags voltage $V (t)$ by $90^{\circ}$
BOver a full cycle the capacitor $C$ does not consume any energy from the voltage source.
CCurrent $I (t)$ is in phase with voltage $V (t)$
DCurrent $I (t)$ leads voltage $V (t)$ by $180^{\circ}$