In YDSE, both slits produce equal intensities on the screen. A 100% transparent thin film is placed in front of one of the slits. Now, the intensity on the centre becomes 75% of the previous intensity. The wavelength of light is 6000Å and refractive index of glass is 1.5. Thus, minimum thickness of the glass slab is
0.2μm
1.0μm
1.4μm
1.6μm
The correct Answer is:D
N//a
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - WAVE OPTICSEXERCISE - Exercise-2 (Part-1)10videos
WAVE OPTICS
- BOOK - RESONANCECHAPTER - WAVE OPTICSEXERCISE - Exercise-2 (Part-2)5videos
WAVE OPTICS
- BOOK - RESONANCECHAPTER - WAVE OPTICSEXERCISE - Exercise-1 (Part-1)13videos
WAVE OPTICS
- BOOK - RESONANCECHAPTER - WAVE ON STRING EXERCISE - Exercise- 3 PART I19videos
WAVE ON STRING
Similar Questions
In YDSE, D = 1.2m and d= 0.25cm, the slits are illuminated with coherent 600nm light. Calculate the distance y above the central maximum for which the average intensity on the screen is 75% of the maximum.
View SolutionA plate of thickness t made of material of refractive index μ is placed in front of one of the slits in a double slit experiment . What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero ?
View Solution
Knowledge Check
- Question 1 - Select One
In YDSE the distance between the slits is 1mm and screen is 25nm away from intensities IF the wavelength of light is 6000A the fringe width on the screen is
A0.15mmB0.30mmC0.24mmD0.12 mm - Question 2 - Select One
A thin perfectly transparent glass sheet of thickness t and refractive index mu is pasted on one of the two identical slits. If the intensity of light at the centre of the screen is I0 in the absence of glass sheet, the intensity at O as a function of thickness of the glass plate is
AI0cos(μtλ)BI0cos2(μtλ)CI0cos2(π(μ−I)tλ)DI0cos(π(μ−I)tλ) - Question 3 - Select One
Minimum thickness of a mica sheet having μ=32 which should be placed in front of one of the slits in YDSE is required to reduce the intensity at the centre of screen to half of maximum intensity is
Aλ/4Bλ/8Cλ/2Dλ/3
In YDSE if a slab whose refractive index can be varied is placed in front of one of the slits. Then, the variation of resultant intensity at mid-point of screen with μ will be best represented by (mu is greater than or equal to 1)
View SolutionIn YDSE, when a glass plate of refractive index 1.5 and thickness t is placed in the path of one of the intefering beams (wavelengthλ), intensity at the position where central maximum occurred previously remains unchanged. The minimum thickness of the glass plate is
View SolutionThe slits in a double-slit interference experiment are illuminated by orange light (λ=60nm). A thin transparent plastic of thickness t is placed in front of one of the slits. The nunber of fringes shifting on screen is plotted versus the refractive index μ of the plastic in graph shown in figure. The value of t is
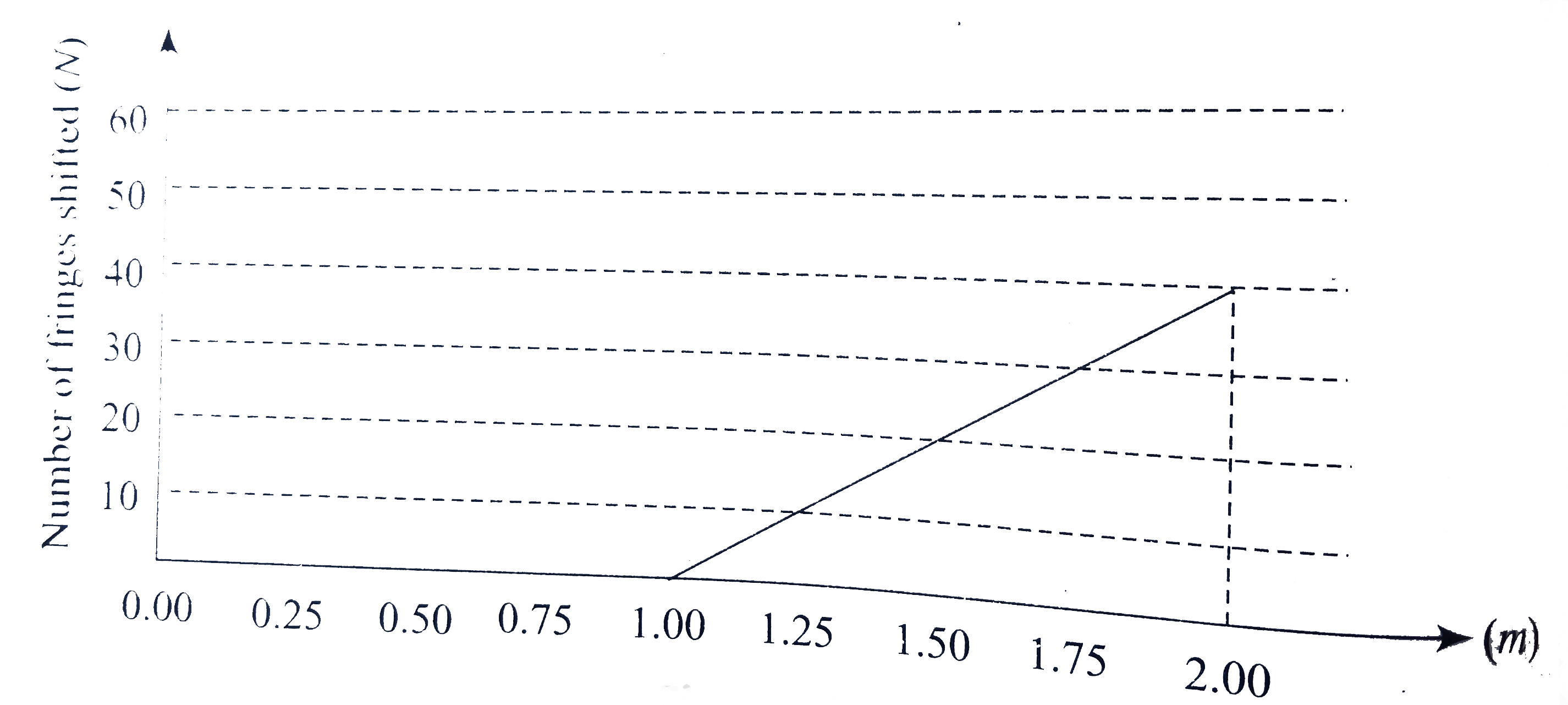 View Solution
View SolutionIn a regular YDSE, when thin film of refractive index mu is placed in front of the upper slit then it is observed that the intensity at the central point becomes half of the original intensity. It is also observed that the initial 3^(rd) maxima is now below the central point and the initial 4th minima is above the central point. Now, a film of refractive index μ1 and thickness same as the above film. is put in the front of the lower slit also. It is observed that whole fringe pattern shifts by one fringe width. What is the value of μ1 ?
View SolutionIn the ideal double-slit experiment, when a glass-plate (refractive index 1.5) of thickness t is introduced in the path of one of the interfering beams (wavelength λ), the intensity at the position where the central maximum occurred previously remains unchanged. The minimum thickness of the glass-plate is
View Solution

