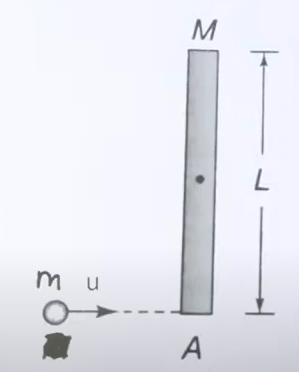
A block of mass m = 1 kg slides with velocity υ=6m/s on a frictionless horizontal surface and collides with a uniform vertical rod and sticks to it as shown. The rod is pivoted about O and swings as a result of the collision making angle θ before momentarily coming to rest. If the rod has mass M = 2 kg, and length l=1m, the value of θ is approximately: (take g=10m/s2)

49∘
63∘
69∘
55∘
The correct Answer is:B
mvl=IΩ
Ω=mvlI
12Iω2=(m+M)glcom(1−cosθ)
12(mvl)2I=(m+M)glcom(1−cosθ)
I=(Ml23+ml2)
I=(23+1)=53
36×32×5=3×10×23=(1−cosθ)
2750=(1−cosθ)
cosθ=1−2750
cosθ=1−2350
θ=60∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
A uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is
 AFB3FC5F4D7F4
AFB3FC5F4D7F4A uniform rod lies at rest on a frictionless horizontal surface. A particle, having a mass equal to that of the rod, moves on the surface perpendicular to the rod collides with it, and finally sticks to it. The minimum loss of KE in the collision , under the given conditions, is
A5%B10%C20%D30%A rod AB of mass M, length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision, the particle comes to rest. The ratio mM is :
Aw2L29v20B9v20w2L2C9v0wLDwL9v0
In the shown figure a mass m slides down the frictionless surface from height h and collides with the uniform vertical rod of length L and mass M after collision the mass m sticks to the rod. The rod is face to rotate in a vertical plane about fixed axis through O. Find the maximum angular deflection of the rod from its initial position.

View SolutionA rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionA rod of length l is pivoted about an end . Find the moment of inertia of the rod about this axis if the linear mass density of rod varies as ρ=ax2+b kg/m
View SolutionA rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m traveling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision the particle comes to rest. Find the ration m/M.
View SolutionA rod AB of mass M, length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision is completely elastic. After the collision, the particle comes to rest. The ratio mM is :
View Solution