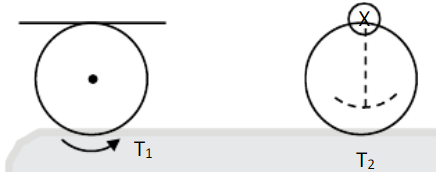
A ring is hung on a nail. It can osicallate without slpping or sliding (i) in its plance with atime period $T_{1}$ and (ii) , back and forth in a direction perpendicular to its plane , with a period $T_{2}$ . The ratio $\frac{T_{1}}{T_{2}}$ will be :

$\frac{2}{\sqrt{3}}$

$\frac{2}{3}$

$\frac{3}{\sqrt{3}}$

$\frac{\sqrt{2}}{3}$

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to find the ratio of the time periods $T_{1}$ and $T_{2}$ for the oscillations of a ring hung on a nail. The ring oscillates in two different modes: (i) in its own plane with a time period $T_{1}$ and (ii) back and forth in a direction perpendicular to its plane with a time period $T_{2}$ .
1. Understanding the System:
- We have a ring of mass $m$ and radius $r$ hung on a nail, allowing it to oscillate in two different modes.
- The oscillation in its own plane (horizontal plane) corresponds to $T_{1}$ .
- The oscillation back and forth in a direction perpendicular to its plane corresponds to $T_{2}$ .
2. Moment of Inertia Calculation:
- For oscillation in the plane of the ring (horizontal plane), we need to find the moment of inertia $I_{1}$ about the vertical axis (the axis through the nail).
- Using the parallel axis theorem, the moment of inertia $I_{1}$ can be calculated as:
$I_{1} = I_{c m} + m d^{2} = \frac{1}{2} m r^{2} + m \cdot r^{2} = \frac{3}{2} m r^{2}$
3. Finding the Time Period $T_{1}$ :
- The angular frequency $ω$ for simple harmonic motion (SHM) is given by:
$ω = \sqrt{\frac{k}{I}}$
- The time period $T_{1}$ is given by:
$T_{1} = 2 π \sqrt{\frac{I_{1}}{k}}$
- Here, $k$ is the effective spring constant for the oscillation in the plane of the ring.
4. Moment of Inertia for Perpendicular Oscillation:
- For oscillation back and forth (perpendicular to the plane), we need to find the moment of inertia $I_{2}$ .
- The moment of inertia $I_{2}$ about the horizontal axis can be calculated as:
$I_{2} = I_{c m} + m d^{2} = \frac{1}{2} m r^{2} + m \cdot {(\frac{r}{2})}^{2} = \frac{1}{2} m r^{2} + \frac{1}{4} m r^{2} = \frac{3}{4} m r^{2}$
5. Finding the Time Period $T_{2}$ :
- The time period $T_{2}$ is given by:
$T_{2} = 2 π \sqrt{\frac{I_{2}}{k}}$
6. Finding the Ratio $\frac{T_{1}}{T_{2}}$ :
- Now we can find the ratio of the time periods:
$\frac{T_{1}}{T_{2}} = \frac{2 π \sqrt{\frac{I_{1}}{k}}}{2 π \sqrt{\frac{I_{2}}{k}}} = \sqrt{\frac{I_{1}}{I_{2}}} = \sqrt{\frac{\frac{3}{2} m r^{2}}{\frac{3}{4} m r^{2}}} = \sqrt{\frac{3 / 2}{3 / 4}} = \sqrt{2} = \frac{2}{\sqrt{3}}$
7. Final Answer:
- Thus, the ratio $\frac{T_{1}}{T_{2}}$ is:
$\frac{T_{1}}{T_{2}} = \frac{2}{\sqrt{3}}$

Updated on:18/9/2024

The point of suspension $λ$ of a simple pendulum with normal time perid $T_{1}$ is moving upward according to equation $y = k t^{2}$ where $k = 1 m / s^{2}$ . If new time period is $T^{2}$ the ratio $\frac{T_{1}^{2}}{T_{2}^{2}}$ will be
A $2 / 3$
B $5 / 6$
C $6 / 5$
D $3 / 2$
A simple pendulum has a time period $T_{1}$ on the surface of earth of radius R. When taken to a height of R above the earth's surface, its time period is $T_{2}$ , ratio $\frac{T_{2}}{T}$ is
A $\frac{1}{\sqrt{2}}$
B $\sqrt{2}$
C2
D4
A ring-1 oscillate with period $T_{1}$ about tangential axis in the plane of ring and an another ring-2 oscillate with period $T_{2}$ about tangential axis tangential axis perpendicular to plane of ring $\frac{T_{1}}{T_{2}}$ ?

A $\sqrt{\frac{3}{4}}$
B $\sqrt{\frac{5}{8}}$
C $\sqrt{\frac{8}{5}}$
D $\sqrt{\frac{4}{3}}$