Initially spring is in natural length and block of mass m is released from rest what should be the minimum value of M (in kg) to just move the 2kg block. If this minimum value is x8kg. Find x

The correct Answer is:6
With respect to free end, velocity of block is 3 m/s leftward. In position of maximum extension, the block will stop w.r.t. free end. As observed from free end, which is inertial frame 12kx2=12mv2
x=√mv2k=3√mk=3√1104=3×10−2 meter = 3 cm
Topper's Solved these Questions
Similar Questions
In the given figure if system is released from rest,then find the minimum value of coefficient of friction such that block A of mass 2m does not move.
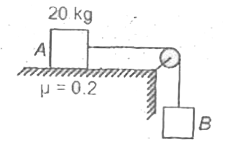
View SolutionIn the figure shown, the coefficient of static friction between the block A of mass 20 kg and horizontal table is 0.2. What should be the minimum mass of hanging block just beyond which blocks start moving?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
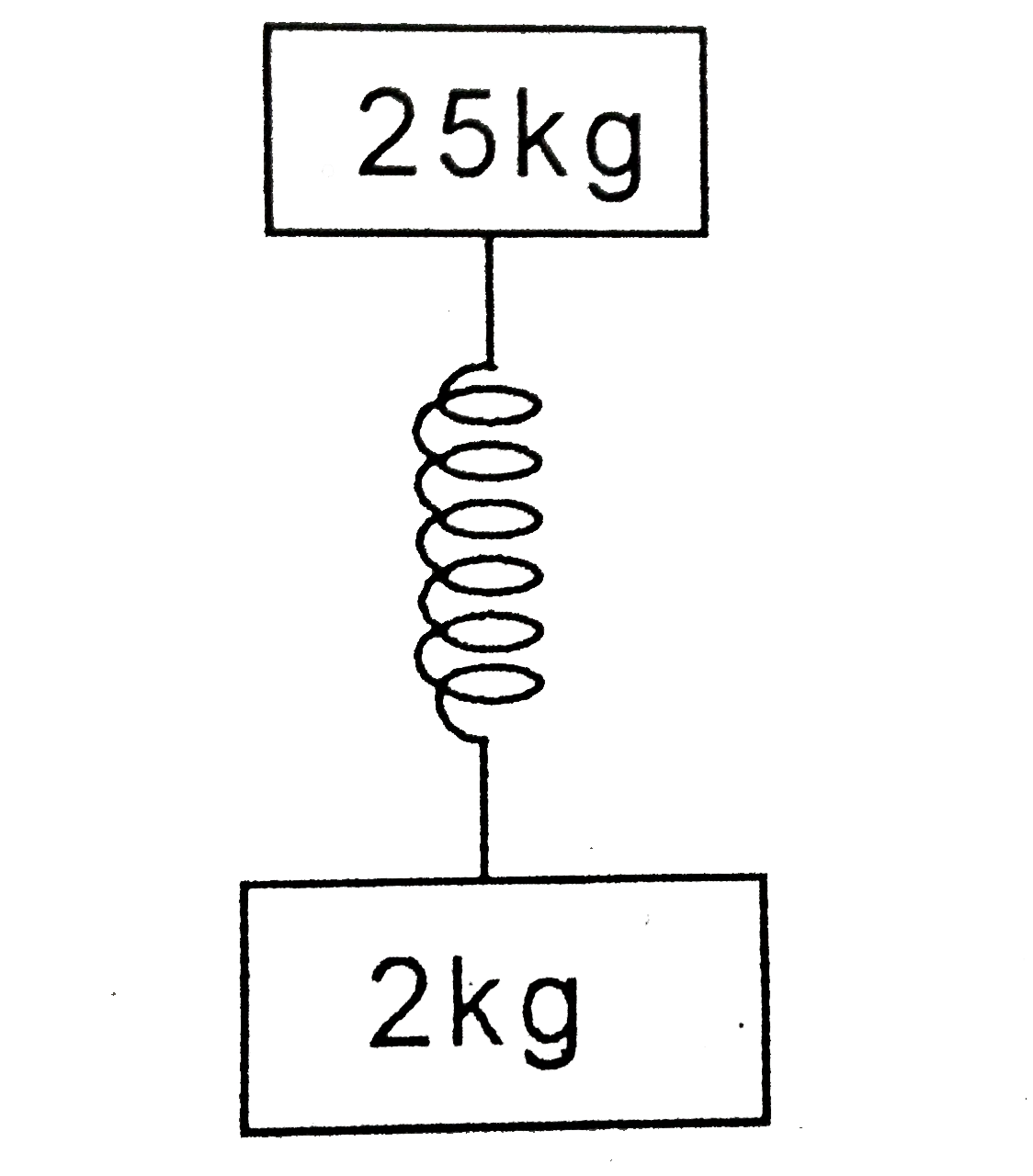
Initialy spring in its natural length now a block at mass 0.25 kg is released then find out maximum force by system on floor ?
 A15 NB20 NC25 ND30 N
A15 NB20 NC25 ND30 N - Question 2 - Select One
A block of mass m is attached with a massless spring of force constant k. The block is placed over a fixed rought inclined surface for which the coefficient of friction is μ=34 . The block of mass m is initially at rest . The block is mass M is released from rest with spring in unstretched state. The minimum value of M required to move the block up the plane is ( neglect mass of string and pulley and friction in pulley )
 A35mB45mC65mD32m
A35mB45mC65mD32m - Question 3 - Select One
What should be the maximum value of M so that the 4 kg block does not slip over the 5 kg block : (Take g=10m/s2)
 A12 kgB8 kgC10 kgD6 kg
A12 kgB8 kgC10 kgD6 kg
What should be minimum value of F so that 2 kg slides on ground but 1kg does not slide on it? [g=10msec2]
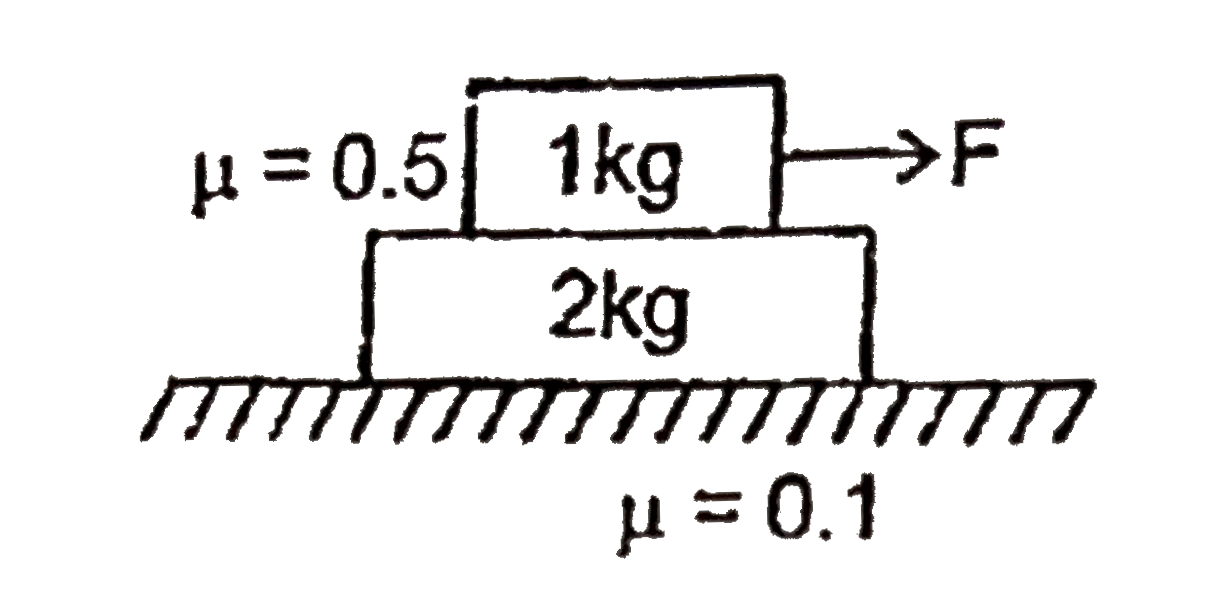 View Solution
View SolutionA block of mass m is dropped onto a spring of constant k from a height h. The second end of the spring is attached to a second block of mass M as shown in figure. Find the minimum value of h so that the block M bounces off the ground. If the block of mass m sticks to the spring immediately after it comes into contact with it.
 View Solution
View SolutionInitially spring is in its natural length . The block of mass 3kg in contact with rigid wall . The block of mass 1kg is pushed through a distance 4cm towards the wall and then released. The velocity of the center of mass when the block of mass 3kg breaks off the wall is (k=100N/m)
 View Solution
View SolutionIn the figure, the ball B is released from rest when the spring is in natural length. For the block A of mass 2m to leave contact with the ground at some instant the minimum mass of B must be
 View Solution
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural lengthView Solution

