A block of mass m tied with a string moves in a vertical plane. A constant vertical upward force F = 3mg (Besides weight mg donward) always acts on the block during its vertical circular motion. What should be the minimum speed (in m/s) at highest point of circle so that the block completes the circular motion. Given length of rod = 25 cm.

Text Solution
The correct Answer is:2
KE at B=12mv2
= loss in PE = mg R (cosα−sinβ)
at B , N = 0, mg sinβ=mv2r
=2mg(cosα−sinβ)
3sinβ=2cosα
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A particle of mass m is tied to a light string of length l and rotated along a vertical circular path. What should be the minimum speed at the highest point of its path so that the string does not become slack at any position ?
A√2glB√glCzeroD√gl/2A stone tied to a string is rotated a vertical circle. The minimum speed of the stone during a complete vertical circular motion.
Ais independent of the mass of the stoneBis independent of the length of the stringCdecreases with increasing mass of the stoneDdecreases with increasing length of the stringA mass m is attached to the end of a rod of length l. The mass goes along a vertical circular path with the other end, hinged at its centre . What should be the minimum speed of mass at the bottom of this circular path
A√4glB√2glC√3glDNone of these
What should be the minimum force P to be applied to the string so that block of mass m just begins to move up the frictionless plane?

View SolutionA block of mass m slides down a smooth vertical circular track. During the motion, the block is in:
View SolutionA block of mass m slides down a smooth vertical circular track. During the motion, the block is in
View SolutionA block of mass m slides down a smooth vertical circular track. During the motion, the block is in
View SolutionTwo point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
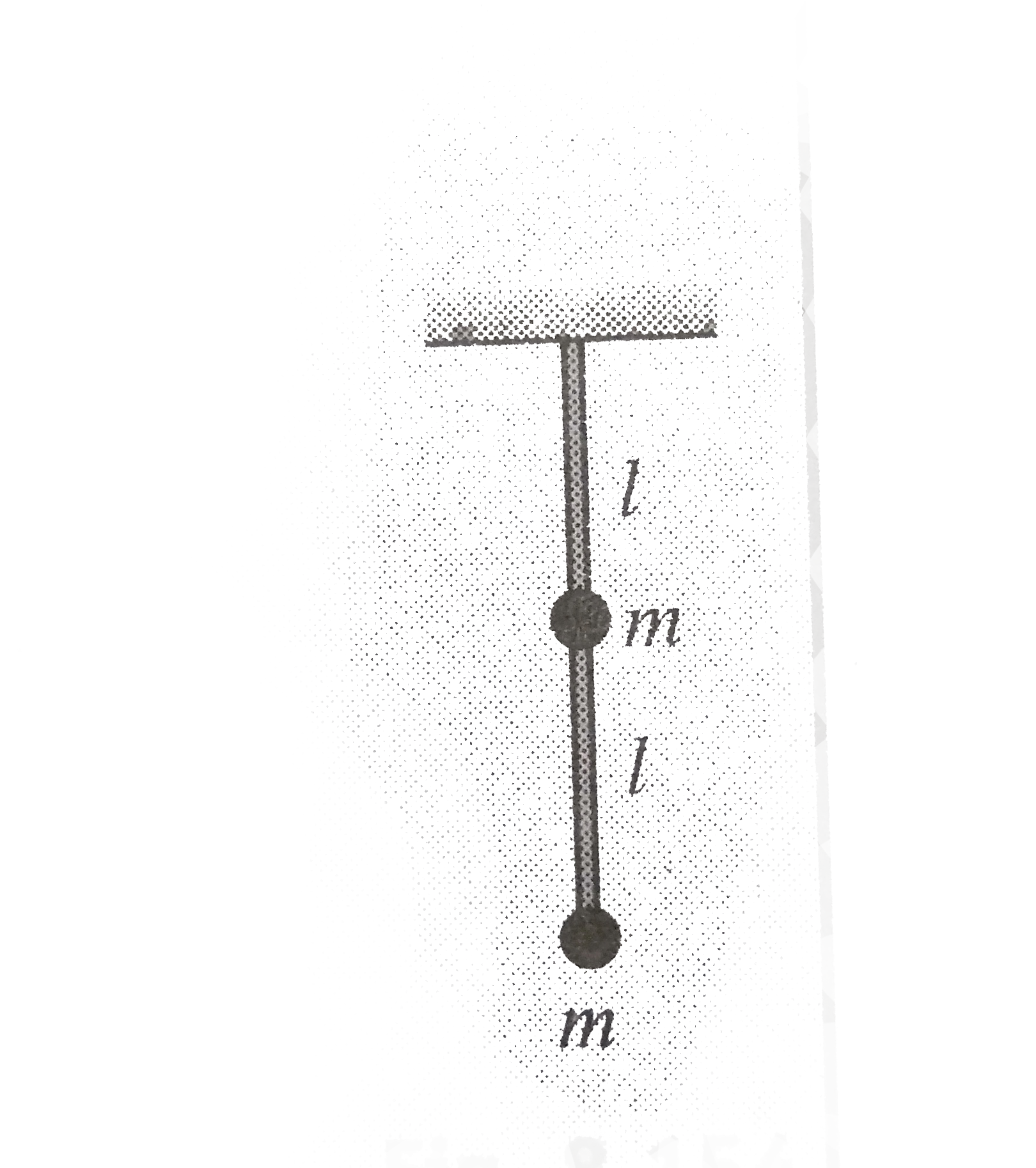
View Solution
