In a meter bridge , the balancing length from left end ( standard resistance of one ohm is in the right gap ) is found to be 20 cm . The value of the unknow resistance is .
0.25Ω
0.8Ω
0.2Ω
0.16Ω
To solve the problem of finding the unknown resistance R using the meter bridge, we can follow these steps:
1. Understand the Setup:
In a meter bridge, when a standard resistance S is placed in one gap and an unknown resistance R is placed in the other gap, the bridge is balanced at a certain length L from one end.
2. Identify Given Values:
- Balancing length L=20cm
- Standard resistance S=1Ω
3. Use the Formula for a Meter Bridge:
The relation for a meter bridge is given by:
RS=L100−L
where L is the balancing length from one end, and 100−L is the length from the other end.
4. Substitute the Known Values:
Substitute L=20cm and S=1Ω into the formula:
R1=20100−20
Simplifying the right side:
R1=2080
5. Calculate the Unknown Resistance:
Now simplify 2080:
2080=14
Thus, we have:
R=14Ω
6. Final Answer:
Therefore, the value of the unknown resistance R is:
R=0.25Ω
In a meter bridge, when a standard resistance S is placed in one gap and an unknown resistance R is placed in the other gap, the bridge is balanced at a certain length L from one end.
- Balancing length L=20cm
- Standard resistance S=1Ω
The relation for a meter bridge is given by:
RS=L100−L
where L is the balancing length from one end, and 100−L is the length from the other end.
Substitute L=20cm and S=1Ω into the formula:
R1=20100−20
Simplifying the right side:
R1=2080
Now simplify 2080:
2080=14
Thus, we have:
R=14Ω
Therefore, the value of the unknown resistance R is:
R=0.25Ω
Similar Questions
Resistance of a wire is, measured using a meter bridge and the balancing length for the unknown resistance of 10ω in the right gap is 48 cm. Find the value of the resistance. If the end corrections are 0.6 cm and 0.4 cm respectively for the left and right ends, find the corrected value of the unknown resistance.
View SolutionIn the metre-bridge experiment with uknown resistance X in the left gap and a known resistance of 60Ω in the right gap, null point is obtained at l cm from left. If the unknown resistance X is shunted by an equal resistance, what should be the value of the known resistance in the right gap in order to get the null point at the same position?.
View Solution
Knowledge Check
In a metere bridge, the balance length from left end (standard resistance of 1Ω is in the right gap) is found to be 20 cm, the length of resistance wire in left gap) is found to be 20 cm the length of resistance wire in left gap is 12 m and radius is 2mm its specific resistance is
Aπ×10−6ohm−mB2π×10−6ohm−mCπ2×10−6ohm−mD3π×10−6ohm−mIn a metre bridge experiment, the balancing length from the left end is found to be 20 cm. If a standard resistance of 20 ohm is kept in the right gap, then the value of the unknown resistance in the left gap is
A5ΩB10ΩC15ΩD7.5ΩIn a metre bridge , the balancing length from the left end is found to be 40cm, when a known resistance of 3Ω is placed in the right gap, then the value of unknown resistance is
A1ΩB2ΩC3ΩD4Ω
An unknown resistance is placed in the left gap and resistance of 50 ohm is placed in the right gap of a meter bridge . The null point is obtained at 40 cm from the left end. Determine the unknown resistance.
View SolutionAn unknown resistance is connected in a left gap of a metre bridge . The balance point is obtained when a resistance of 10Ω is taken out from the resistance box in the right gap. On increasing the resistance from the resistance box by 12.5Ω the balance point shifts by 20 cm.
find the unknown resistance.
View SolutionIn a meter-bridge experiment with a resistance R1 in left gap and a resistance X in a right gap. null point is obtained at 40cm from the left emf. With a resistance R2 in the left gap, the null point is obtainned at 50cm from left hand. Find the position of the left gap is containing R1 and R2 (i) in series and (ii) in parallel.
View SolutionIn meter bridge , the balancing length from left is found to be 20 cm when standard connected of 1Ω is in right gap . The value of unknown resistance is
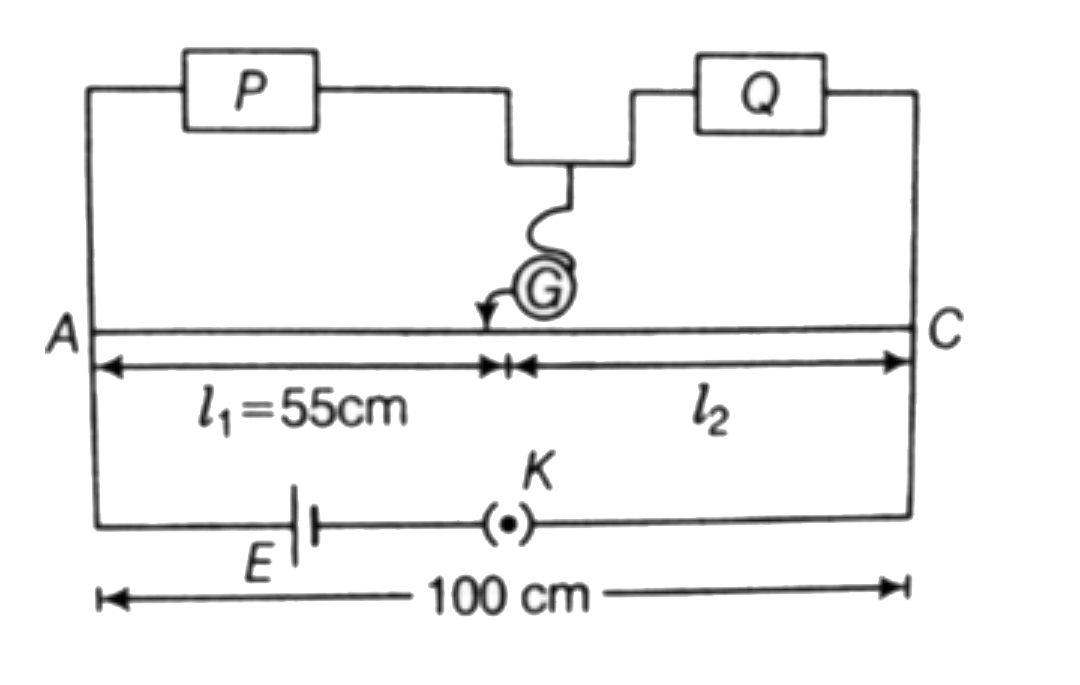
View SolutionIn a meter bridge experiment, resistances are connected as shown in figure. The balancing length l1=55cm. Now, an unknown resistance x is connected in series with P and the new balancing length is found to be 75 cm. What is the value of The value of 11x (in ohm)? (Given, P=4Ω)
View Solution
