Tow cells of emf $E_{1}$ and $E_{2} (E_{1} > E_{2})$ are connected individually to a potentiometer and their corresponding balancing length are 625 cm and 500 cm, then the ratio $\frac{E_{1}}{E_{2}}$ is .

A

$5 : 4$

B

$3 : 1$

C

$5 : 1$

D

$4 : 5$

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:A

To solve the problem, we need to find the ratio of the EMFs $\frac{E_{1}}{E_{2}}$ using the balancing lengths measured on a potentiometer.
1. Understanding the Potentiometer Principle:
- When two cells are connected to a potentiometer, the EMF of each cell is proportional to the balancing length measured on the potentiometer.
- The relationship can be expressed as:
$E_{1} = Φ L_{1} and E_{2} = Φ L_{2}$
where $Φ$ is the potential gradient, $L_{1}$ is the balancing length for $E_{1}$ , and $L_{2}$ is the balancing length for $E_{2}$ .
2. Setting Up the Ratio:
- From the above equations, we can derive the ratio of the EMFs:
$\frac{E_{1}}{E_{2}} = \frac{Φ L_{1}}{Φ L_{2}}$
- The $Φ$ cancels out, leading to:
$\frac{E_{1}}{E_{2}} = \frac{L_{1}}{L_{2}}$
3. Substituting the Values:
- We know from the problem statement that:
- $L_{1} = 625 cm$
- $L_{2} = 500 cm$
- Substituting these values into the ratio gives:
$\frac{E_{1}}{E_{2}} = \frac{625}{500}$
4. Simplifying the Ratio:
- To simplify $\frac{625}{500}$ :
$\frac{625}{500} = \frac{625 \div 125}{500 \div 125} = \frac{5}{4}$
5. Final Result:
- Therefore, the ratio of the EMFs is:
$\frac{E_{1}}{E_{2}} = \frac{5}{4}$
Final Answer:
$\frac{E_{1}}{E_{2}} = \frac{5}{4}$

|

Updated on:18/9/2024

Class 12 PHYSICS CURRENT ELECTRICITY

Similar Questions

Knowledge Check

Question 1 - Select One
Two cells of emf $E_{1}$ and $E_{2} (E_{1} > E_{2})$ are connected in series to potentiometer for balancing length 625 cm . When polarity of $E_{2}$ is reversed then balancing length becomes 125 cm. Then the ratio $\frac{E_{1}}{E_{2}}$ is
A $3 : 2$
B $3 : 1$
C $5 : 1$
D $2 : 1$
Question 2 - Select One
Two cells of emfs $E_{1}$ and $(E_{2} (E_{1} > E_{2})$ are connected as shows in Fig. $6.45$ .

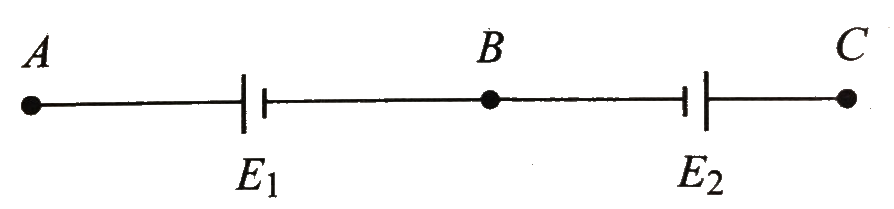
When a potentiometer is connected between $A$ and $B$ , the balancing length of the potentiometer wire is $300 c m$ . On connecting the same potentiometer between $A$ and $C$ , the balancing length is $100 c m$ . The ratio $E_{1} / E_{2}$ is
A $3 : 1$
B $1 : 3$
C $2 : 3$
D $3 : 2$
Question 3 - Select One
Two cells of E.M.F. $E_{1}$ and $E_{2} (E_{2} > E_{1})$ are connected in series in the secondary circuit of a potentiometer experiment for determination of E.M.F. The balancing length is found to be 825 cm. Now when the terminals to cell $E_{1}$ are reversed, then the balancing length is found to be 225 cm. The ratio of $E_{1}$ and $E_{2}$ is
A $2 : 3$
B $4 : 7$
C $7 : 4$
Dnone of these

Recommended Questions

Home
Ask Doubt
Profile