Effect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
For exothermic reaction if ΔS∘<0 then the sketch of log k vs 1T may be
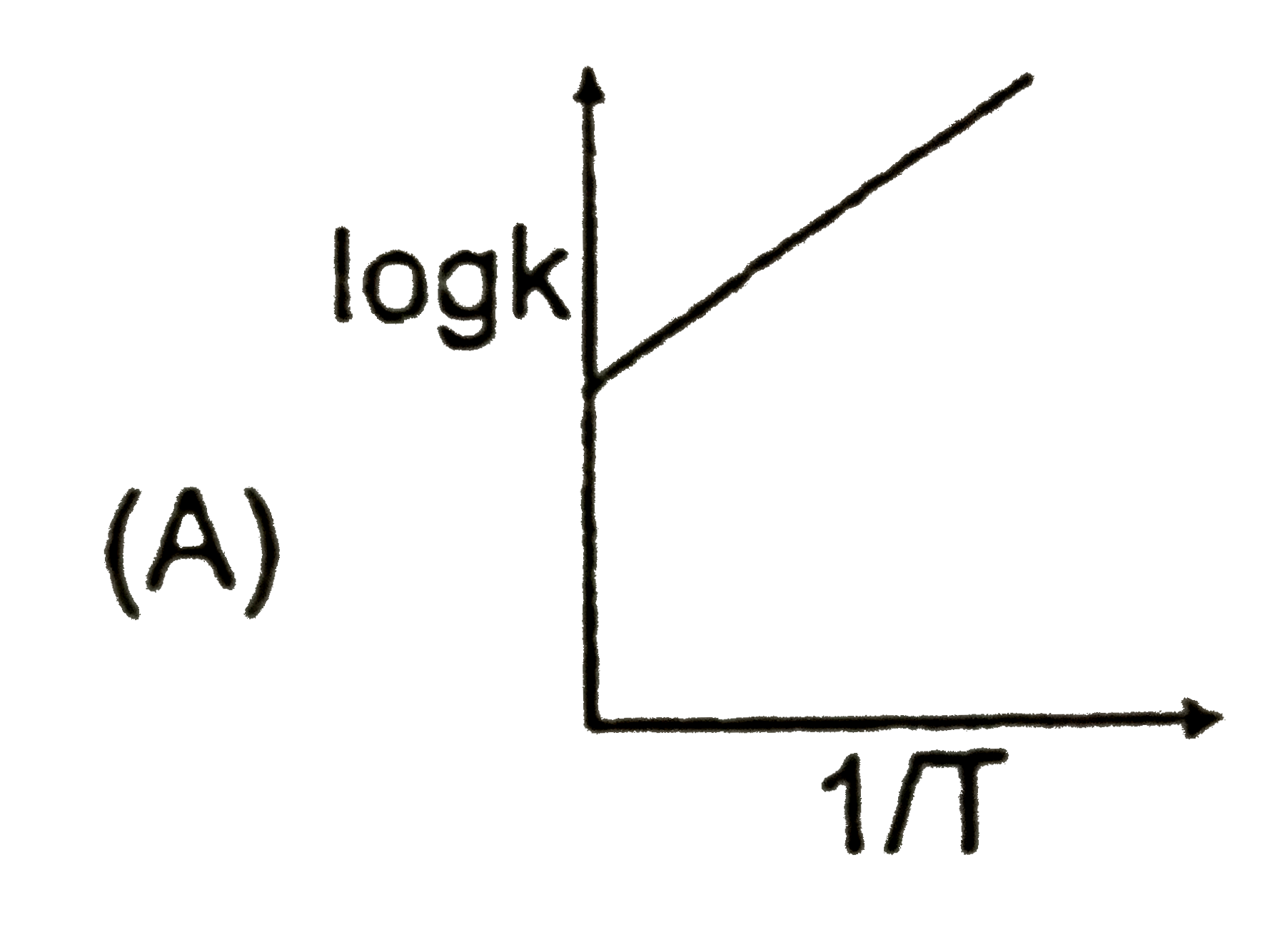
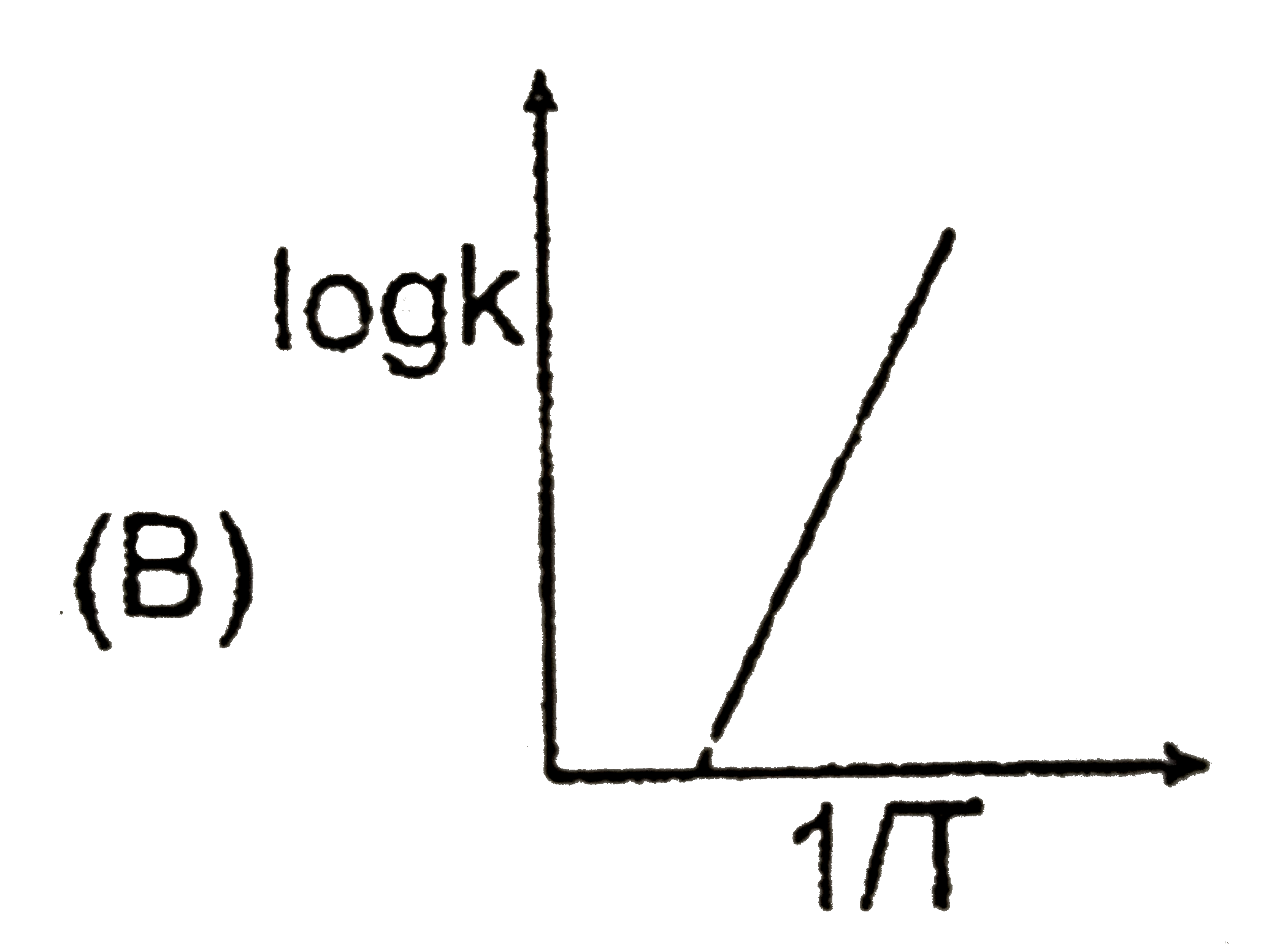

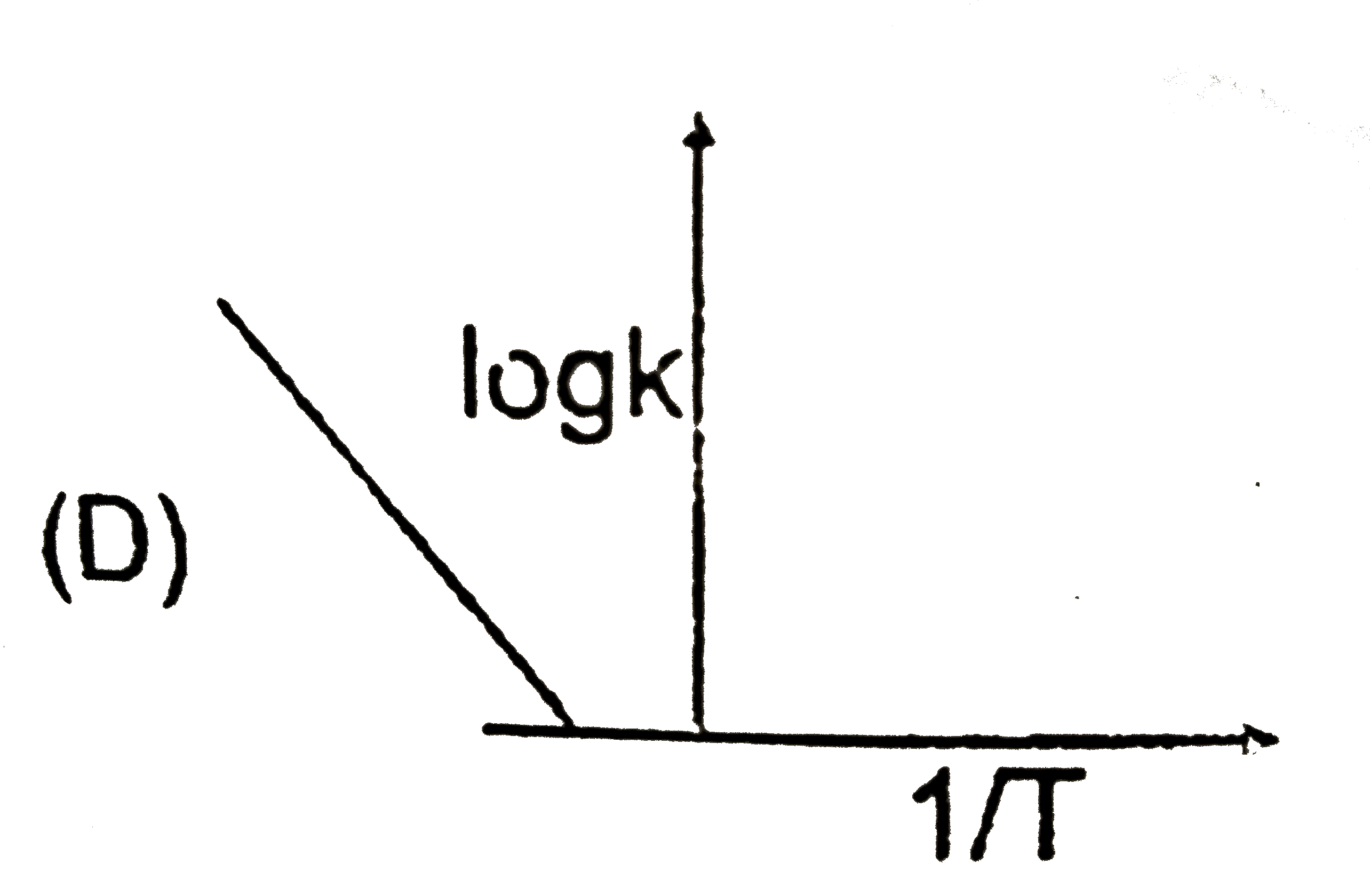
The correct Answer is:B
Step by step video, text & image solution for Effect of temperature on the equilibrium process analysed by using the thermodynamics From the thermodynamics reaction DeltaG^(@)=-2.30RTlogk DeltaG^(@): Standing free energy change DeltaG^(@)=DeltaH^(@)-TDeltaS^(@)…(ii) DeltaH^(@) :Standard heat of the reaction gt From eqns.(i) and(ii) -2RTlogk=DeltaH^(@)=TDeltaS^(@) DeltaS^(@) : standard entropy change implies" "logK=-(DeltaH^(@))/(2.3RT)+(DeltaS^(@))/(2.3R) Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =(-DeltaH^(@))/(2.3R) amd y intercept =(DeltaS^(@))/(2.3R) If at temperature T_(1) equilibrium constant be k_(1) and at temperature T_(2)equilibrium constant be k_(2) then : implies" "logK_(1)=-(DeltaH^(@))/(2.3RT_(1))+(DeltaS^(@))/(2.3R)..(iv) implies" "logK_(2)=-(DeltaH^(@))/(2.3RT_(2))+(DeltaS^(@))/(2.3R)...(v) Substracting e.q (iv) from (v), we get from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction For exothermic reaction if DeltaS^(@)lt0 then the sketch of log k vs (1)/(T) may be by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise-3 (Part-1)6videos
CHEMICAL EQUILIBRIUM
- BOOK - RESONANCECHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise-3 (Part-2)17videos
CHEMICAL EQUILIBRIUM
- BOOK - RESONANCECHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise-2 (Part-3)34videos
CHEMICAL EQUILIBRIUM
- BOOK - RESONANCECHAPTER - CHEMICAL BONDINGEXERCISE - Inorganic chemistry (Chemistry Bonding)49videos
CHEMICAL BONDING
- BOOK - RESONANCECHAPTER - D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS EXERCISE - Match the column1videos
D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS
Similar Questions
At constant temperature, the equilibrium constant (Kp) for the decomposition reaction
N2O4⇔2NO2
is expressed by Kp=4x2p/(1−x2), where p=pressure x= extent of decomposition. Which of the following statements is true?01:30View SolutionIn which of the following equilibrium, change in the volume of the system does not alter the number of moles?
06:25View SolutionWhich of the following is correct about the chemical equilibrium ?
06:25View SolutionWhich is correct order ofr net dipole moment :
06:25View SolutionMatch the reactions in Column I with the types of products/the use of products in Column II.
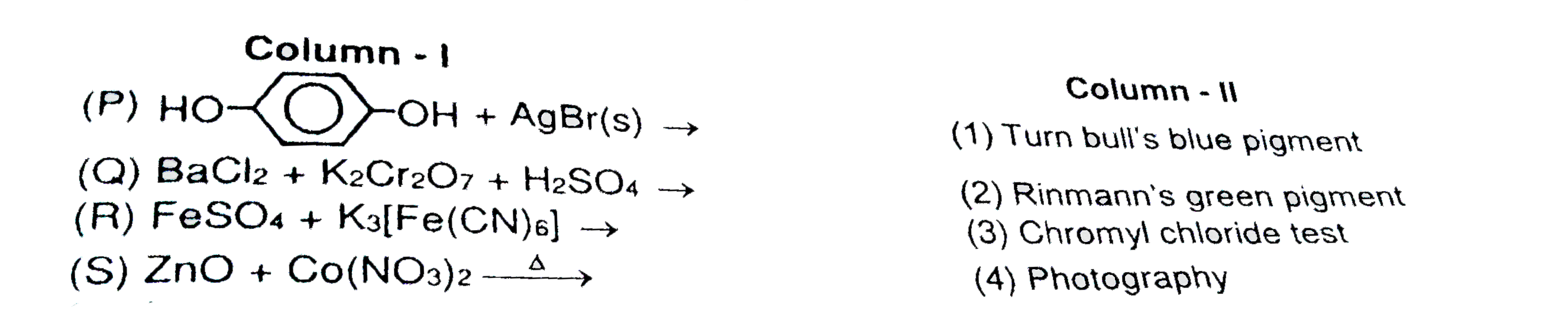 02:42View Solution
02:42View SolutionΔG=ΔH−TΔS and ltBRgt ΔG=ΔH+T[d(ΔG)dT]p, then(dEcelldT) is
05:06View SolutionEffect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
If statndard heat of dissociation of PCl5 is 230 cal then slope of the graph of log vs 1T is :02:20View SolutionEffect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
For exothermic reaction if ΔS∘<0 then the sketch of log k vs 1T may be04:34View SolutionEffect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
If for a particular reversible reaction
KC=57 abd 355∘C and KC=69 at 450∘C then02:42View SolutionThe relation ΔG=ΔH−TΔS was given by
01:43View Solutionसमीकरण ΔG=ΔH−TΔS की व्युत्पत्ति कीजिए ।
04:35View SolutionFor a process at a particular temperature and pressure, DeltaG=DeltaH-TDeltaS . It can be written as: -DeltaG=T[-(DeltaH)/(T)+DeltaS] . What does the quantity within the bracket indicate?
View SolutionIf DeltaG=DeltaH-TDeltaS and DeltaG = DeltaH+T[(d(DeltaG))/(dT)] , then variation EMF of a cell E, with temperature T, is given by
View SolutionThe relation ΔG=ΔH−TΔS was given by
02:43View SolutionΔG=ΔH−TδSandΔG=ΔH+T[d(ΔG)dT] then (dEcelldT) is
02:36View SolutionEstablish DeltaG = DeltaH- TDeltaS .
01:59View Solution

