The quantities of heat required to raise the temperature of two solid copper spheres of radii r1 and r2 (r1=1.5r2) through 1K are in ratio
27/8
44078
43892
43954
To solve the problem of finding the ratio of heat required to raise the temperature of two solid copper spheres of radii r1 and r2 (where r1=1.5r2) through 1K, we can follow these steps:
1. Understand the Heat Required Formula:
The heat Q required to raise the temperature of an object is given by the formula:
Q=m⋅C⋅ΔT
where:
- m is the mass of the object,
- C is the specific heat capacity of the material,
- ΔT is the change in temperature.
2. Determine the Mass of the Spheres:
The mass m of a sphere can be calculated using the formula:
m=ρ⋅V
where ρ is the density of the material and V is the volume of the sphere. The volume V of a sphere is given by:
V=43πr3
Therefore, the mass of the spheres can be expressed as:
m1=ρ⋅43πr31
m2=ρ⋅43πr32
3. Substitute Radii:
Given r1=1.5r2, we can express m1 in terms of r2:
m1=ρ⋅43π(1.5r2)3=ρ⋅43π(3.375r32)=3.375⋅ρ⋅43πr32
Thus, we have:
m1=3.375m2
4. Calculate Heat for Each Sphere:
The heat required to raise the temperature of each sphere by 1K is:
Q1=m1⋅C⋅1=3.375m2⋅C
Q2=m2⋅C⋅1=m2⋅C
5. Find the Ratio of Heat Required:
Now, we can find the ratio of the heat required for the two spheres:
Q1Q2=3.375m2⋅Cm2⋅C=3.375
Final Result:
The ratio of the quantities of heat required to raise the temperature of the two solid copper spheres through 1K is:
Q1Q2=3.375:1
The heat Q required to raise the temperature of an object is given by the formula:
Q=m⋅C⋅ΔT
where:
- m is the mass of the object,
- C is the specific heat capacity of the material,
- ΔT is the change in temperature.
The mass m of a sphere can be calculated using the formula:
m=ρ⋅V
where ρ is the density of the material and V is the volume of the sphere. The volume V of a sphere is given by:
V=43πr3
Therefore, the mass of the spheres can be expressed as:
m1=ρ⋅43πr31
m2=ρ⋅43πr32
Given r1=1.5r2, we can express m1 in terms of r2:
m1=ρ⋅43π(1.5r2)3=ρ⋅43π(3.375r32)=3.375⋅ρ⋅43πr32
Thus, we have:
m1=3.375m2
The heat required to raise the temperature of each sphere by 1K is:
Q1=m1⋅C⋅1=3.375m2⋅C
Q2=m2⋅C⋅1=m2⋅C
Now, we can find the ratio of the heat required for the two spheres:
Q1Q2=3.375m2⋅Cm2⋅C=3.375
The ratio of the quantities of heat required to raise the temperature of the two solid copper spheres through 1K is:
Q1Q2=3.375:1
Topper's Solved these Questions
Similar Questions
Solve the foregoing problem for the case of two concentric spheres of radii R1 and R2 and temperatures T1 and T2.
View SolutionThe magnitude of gratitational field intensities at distance r1 and r2 from the centre of a uniform solid sphere of radius R and mass M are I1 and I2 respectively. Find the ratio of I1/I2 if (a) r1>R and r2>R and (b) r1<R and r2<R (c ) r1>R and r2<R.
View Solution
Knowledge Check
The quantities of heat required to raise the temperature of two solid copper spheres of radii r1 and r2 (r1=1.5r2) through 1K are in ratio
A94B32C53D278The capacitance of two concentric spherical shells of radii R1 and R2(R2>R1) is
A4πε0R2B4πε0(R2−R1)R1R2C4πε0R1R2(R2−R1)D4πε0R1Two conducting spheres of radii r1 and r2 are equally charged. The ratio of their potentral is-
Ar21/r22Br22/r21Cr1/r2Dr2/r1
Three circles of radii r1,r2andr3 are drawn concentric to each other. The radii r1 and r2 are such that the area of the circle with radius r1 is equal to the area between the circle of radius r2 and r1 . The area between the circle of radii r2 and r3 is equal to area between the circle of radii r2 and rr . What is the value of r1:r2:r3 ?
View SolutionThe figure shows a system of two concentric spheres of radii r1andr2 are kept at temperature T1andT2, respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to
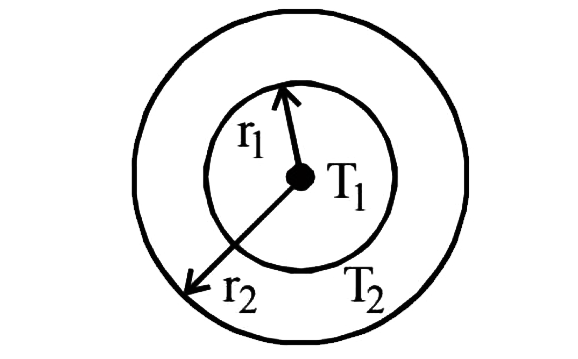
View SolutionThe concentric, thin metallic spheres of radii r1 and r2(r1>r2) carry charges q1 and q2 respectively. Then the electric potential at distance r(r2<r<r1) will be 14πε0 times
View SolutionIf the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then
View SolutionTwo satellites of masses m1 and m2(m1>m2) are revolving around earth in circular orbits of radii r1 and r2(r1>r2) respectively. Which of the following statements is true regarding their velocities V1 and V2
View Solution
