In line segment EF, if G is mid-point of EF then
EF=FG
EG=FE
EG=FG
EG=EF
The correct Answer is:C
Similar Questions
In the figure, ABCD is a square and EF is parallel to the line BD. R is the mid-point of the line EF. Prove: BE=DE
03:09View SolutionIn the figure, ABCD is a square and EF is parallel to the line BD. R is the mid-point of the line EF. Prove: AR bisects BAD angle
07:34View SolutionIn the figure, ABCD is a square and EF is parallel to the line BD. R is the mid-point of the line EF. Prove: If AR is increased it will pass through C.
04:49View Solutionआकृति में, ABCD एक समलम्ब चतुर्भुज हैं, जिसमें भुजा AB भुजा DC के समान्तर हैं तथा E भुजा AD का मध्य-बिंदु हैं। E भुजा BC पर इस प्रकार है खंड EF, भुजा DC के समान्तर हैं। सिद्ध कीजिए कि EF=12(AB+DC)
04:09View SolutionDraw a line segment EF equal to a given line segment AB
01:30View SolutionIn the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF. Show that : EF = AC.
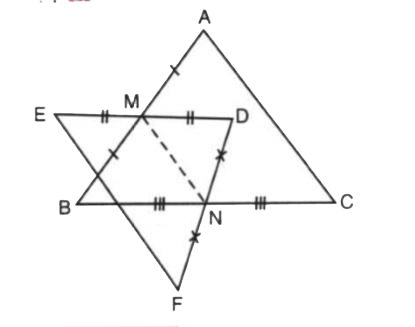 06:29View Solution
06:29View SolutionThe sides AB and AC are equal of an isosceles triangle ABC. D E and F are the mid-points of sides BC, CA and AB respectively. Prove that:
(i) Line segment AD is perpedicular to line segment EF.
(ii) Line segment AD bisects the line segment EF.05:56View SolutionIn trapezium ABCD. AB||DC and DC = 2AB. A line segment EF drawn parallel to AB cuts AD in F and BC in E such that BEEC=34 .
Diagonal DB intersects EF at G. prove that &EF= 10AB.
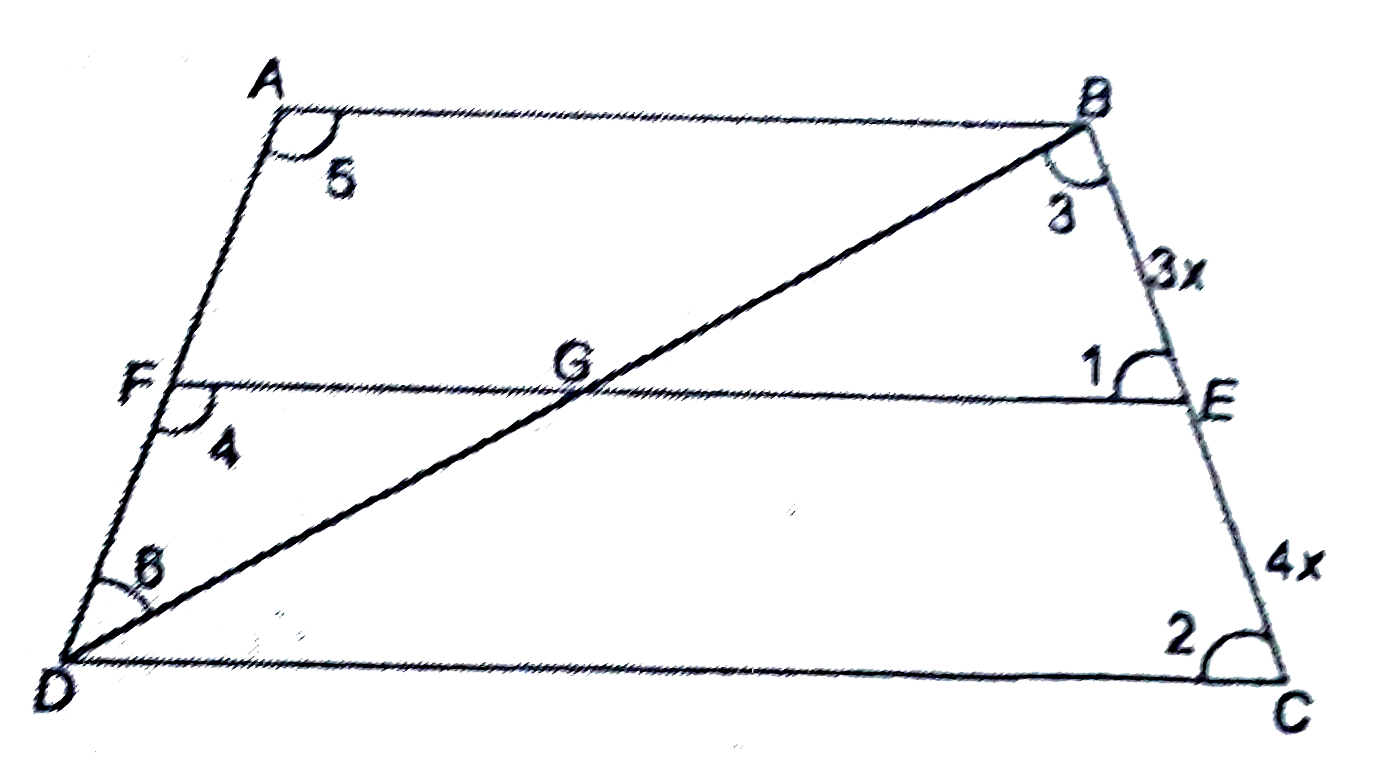 04:18View Solution
04:18View Solution

