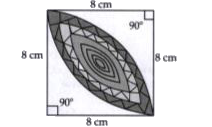
Calculate the area of the designed region in Fig. 12.34 common between the two quadrants of circles of radius 8 cm each.
Video Solution
Text Solution
as we can see that
ar(2 quad) = area (square) + ar(design)
ar(design) = 2* ar(quadrant) - ar(square)
=2⋅14⋅πr2−r2
=πr22−r2
=r2(π2−1)
=82(12⋅227−1)
=6411−77
=2567cm2
answer
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
The area of the square inscribed in a circle of radius 8 cm is
A256 sq. cmB250 sq. cmC128sq. CmD125 sq. cm
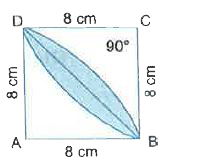
Calculate the area of the designed region in common between the two quadrants of circles of radius 8 cm each.
 View Solution
View SolutionCalculate the area of the designed region in fig. 15.55 common between two quadrilate of circles of radius 8 cm each.
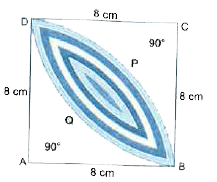
View SolutionCalculate the area of the designed region in Fig. 12.29, which is compon between the two quadtants of circles of radius, 8 cm each.
 View Solution
View SolutionCalculate the area of the designed region in the given figure, common between two quadrants of circles of radius 7cm each.
 View Solution
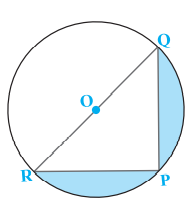
View SolutionFind the area of the shaded region in Fig. 12.19, if PQ=24 cm, PR=7 cm and O is the centre of the circle.
 View Solution
View SolutionThe area of a square inscribed in a circle of radius 8 cm is:
View SolutionThe perimeter of the quadrant of a circle is 25 cm. Find the area.
View Solution