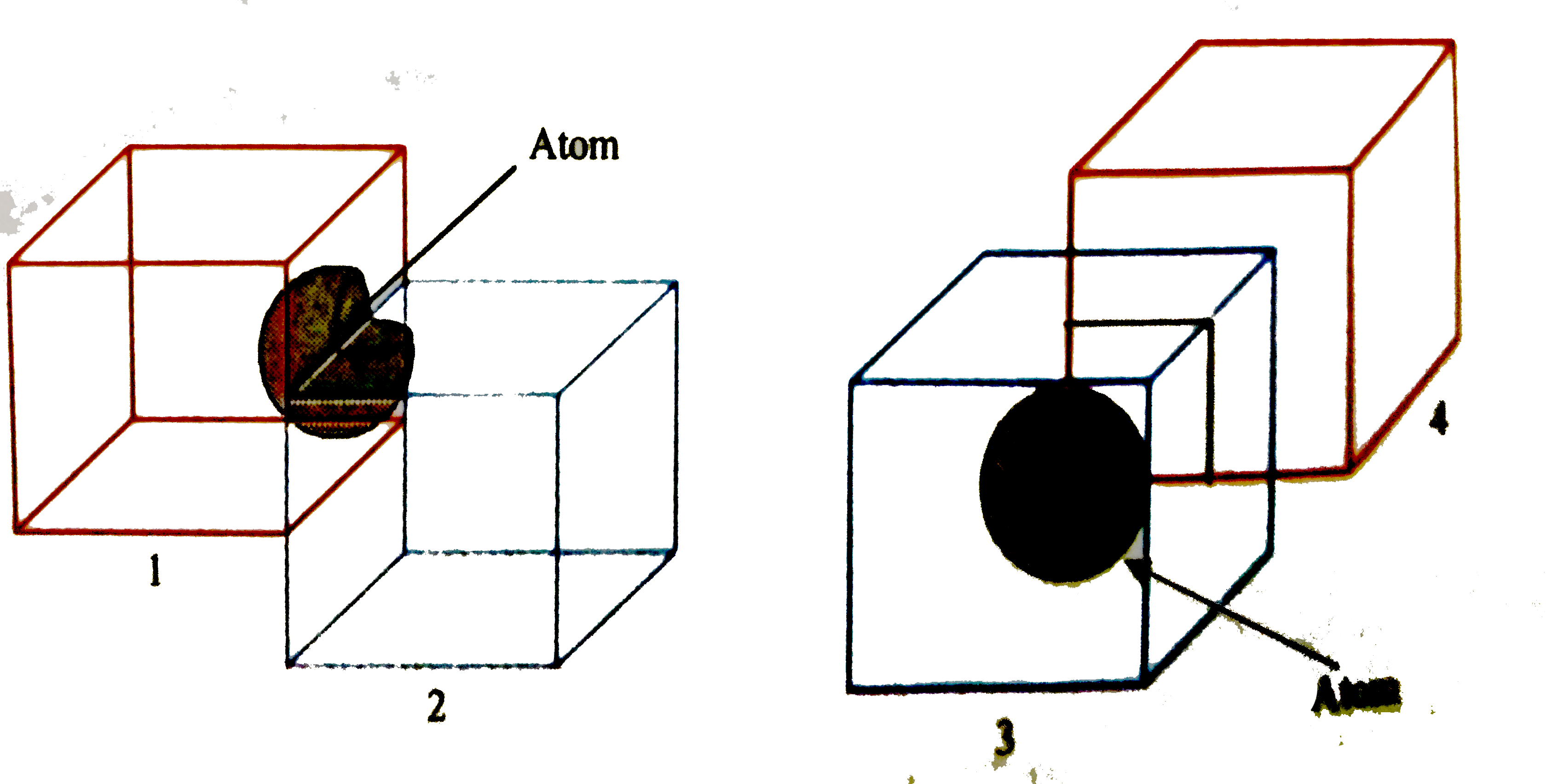
Following diagrams show identical cubes such that edge of cube 2 lies exactly in the middle of one of the faces of Cube1 and Cube 4 has a corner at the body centre of the Cube3. Find the contributions (in fraction) of the spheres shown to each of the cubes

Text Solution
The correct Answer is:Cube1 - 1/2; Cube 2 - 1/4; Cube3 - 1; Cube4 - 1/8
|
Topper's Solved these Questions
- SOLID STATEBOOK - RESONANCECHAPTER - SOLID STATEEXERCISE - Part-II : Only one option correct type
42 Videos
- SOLID STATEBOOK - RESONANCECHAPTER - SOLID STATEEXERCISE - Part-III : Match the column
3 Videos
- SOLID STATEBOOK - RESONANCECHAPTER - SOLID STATEEXERCISE - Miscellaneous solved problems
16 Videos
- S BLOCK ELEMENTSBOOK - RESONANCECHAPTER - S BLOCK ELEMENTSEXERCISE - INORGANIC CHEMISTRY(s-Block Elements)
36 Videos
- STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYBOOK - RESONANCECHAPTER - STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYEXERCISE - Section -B
18 Videos
Similar Questions
Knowledge Check
Following frightening diagrams show identical cubes such that edge of cube 2 lies exactly in the middle of one of the faces of Cube 1 and Cube 4 has a corner at the body centre of the cube 3 . Find the contribution (in fraction) of the spheres shown to each of the cube 1 ,2 , 3 and 4 respectively is
 A12,14,1,18B12,14,18,1C18,14,1,12D18,14,12,1
A12,14,1,18B12,14,18,1C18,14,1,12D18,14,12,1If each edge of a cube is 6 cm, then find the diagonal of cube.
A6√2cmB6√3cmC36√2cmD36√3cmA charge 'Q' is placed at each corner of a cube of side 'a'. The potential at the centre of the cube is
A8Qπε0aB4Q4πε0aC4Q√3πε0aD2Qπε0a
If a point charge q is placed at the centre of a cube.
What is the flux linked (a) with the cube? (b) with each face of the cube?
View SolutionIf a point charge q is placed at the centre of a cube.
What is the flux linked (a) with the cube? (b) with each face of the cube?
View SolutionIf the edge length of the side of a cube is a, the distance between the body centred atom and one corner atom in the cube will be:
View SolutionThe packing fraction for a body-centred cube is
View SolutionThe packing fraction for a body-centred cube is
View Solution
