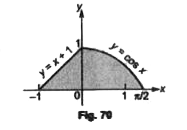
The area of the figure bounded by right of the line $y = x + 1, y = cos x$ and x-axis is :

A

$\frac{1}{2}$

B

$\frac{2}{3}$

C

$\frac{5}{6}$

D

$\frac{3}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

|

Answer

Step by step video, text & image solution for The area of the figure bounded by right of the line y = x + 1, y= cos x and x-axis is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS DEFINITE INTEGRAL

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
What is the area of the region bounded by stratight line 9 x + 4y = 36 , x - axis and the y - axis ?
A12 sq. units
B18 sq. units
C16 sq. units
D15 sq. units
Question 2 - Select One
Determine the area of the figure bounded by two branches of the curve ${(y - x)}^{2} = x^{3}$ and the straight line $x = 1$ .
A $\frac{4}{5}$ sq units
B $\frac{4}{7}$ sq units
C $\frac{4}{9}$ sq units
D $\frac{4}{11}$ sq units
Question 3 - Select One
The area of the region bounded by the curves $y = x^{3}, y = \frac{1}{x}, x = 2$ and x - axis (in sq. units) is
A $4 - {log}_{e} 2$
B $\frac{1}{4} + {log}_{e} 2$
C $3 - {log}_{e} 2$
D $\frac{15}{4} - {log}_{e} 2$

RESONANCE-DEFINITE INTEGRATION & ITS APPLICATION -Exercise 1 Part-II

Home
Ask Doubt
Profile