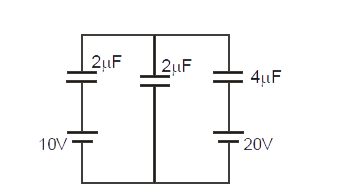
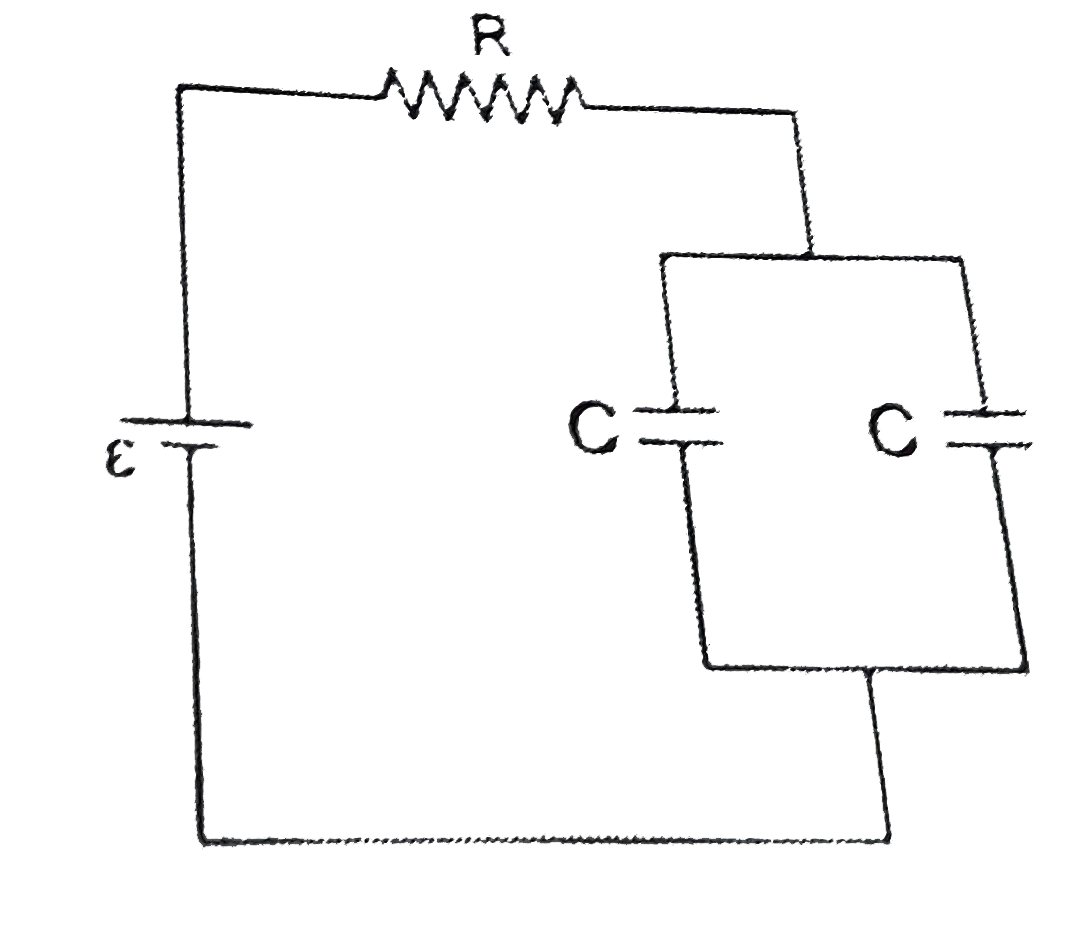
Without using the formula of equivalent. Find out charge on capacitor and current in all the branches as a function of time.
Video Solution
Text Solution
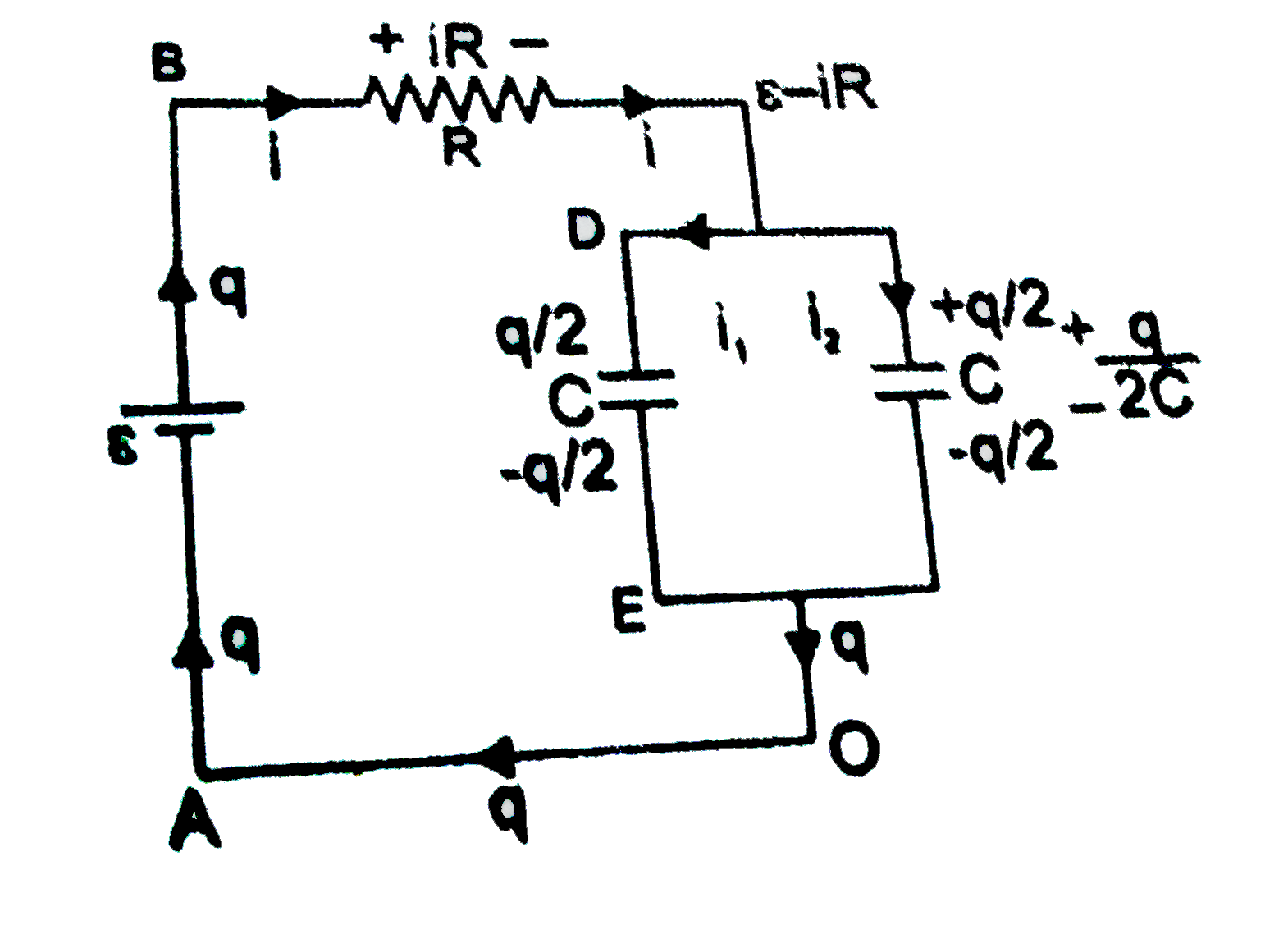
ε−iR=q2C
i=εR−q2RC=2Cε−q2CR
dq2εC−q=dt2CR
∫q0dq(2εC−q)=t2CR
2εC−q2εC=e−t/2RC
q=2εC(1−e−t/2RC)
q1=q2=εC(1−e−t/2RC)⇒i1=ε2Re−t/2RC
q2=q2=εC(1−e−t/2RC)⇒i2=ε2Re−t/2RC
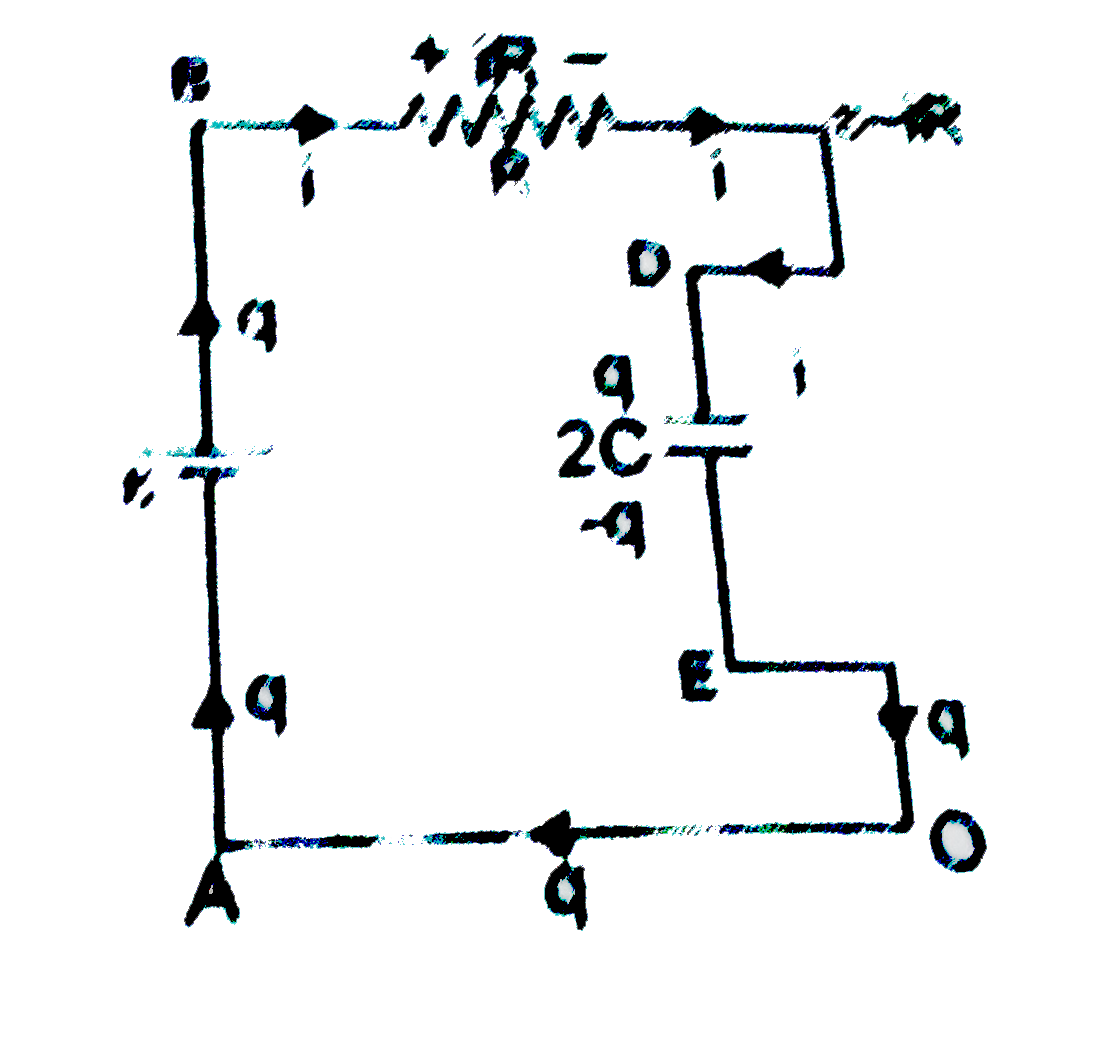
Alternate solution
by equivalent
Time constant of circuit =2C×R=2RC
maximum charge on capacitor =2C×ε=2Cε
Hence equations of charge and current are as given below
q=2εC(1−e−t/2RC)
q1=q2=εC(1−e−t/2CR)⇒i1=ε2Re−t/2CR
q2=q2=εC(1−e−t/2RC)⇒i2=ε2Re−e−t/2RC
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - CAPACITANCEEXERCISE - Miscellaneous Solved Example3videos
CAPACITANCE
- BOOK - RESONANCECHAPTER - CAPACITANCEEXERCISE - Exercise - 179videos
CAPACITANCE
- BOOK - RESONANCECHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems17videos
ATOMIC PHYSICS
- BOOK - RESONANCECHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 313videos
COMMUNICATION SYSTEMS
Similar Questions
Knowledge Check
- Question 1 - Select One
Find current in the branch CD of the circuit
 A15AB35AC10AD25A
A15AB35AC10AD25A
Find charge on each capacitor.
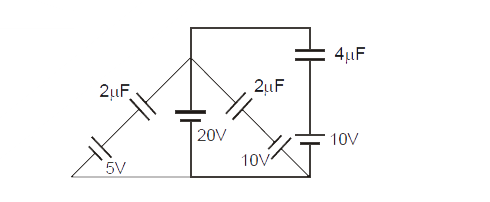 View Solution
View SolutionFind charge in each capacitor:
View SolutionFind charge in each capacitor:
View Solution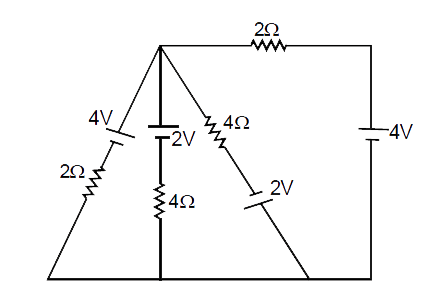
Find the current in every branch ?View Solution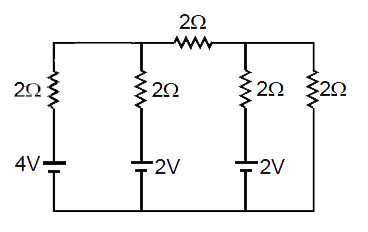
Find the current in every branch ?View Solution
Find the current in every branch ?View SolutionFind the charge stored in the capacitor.
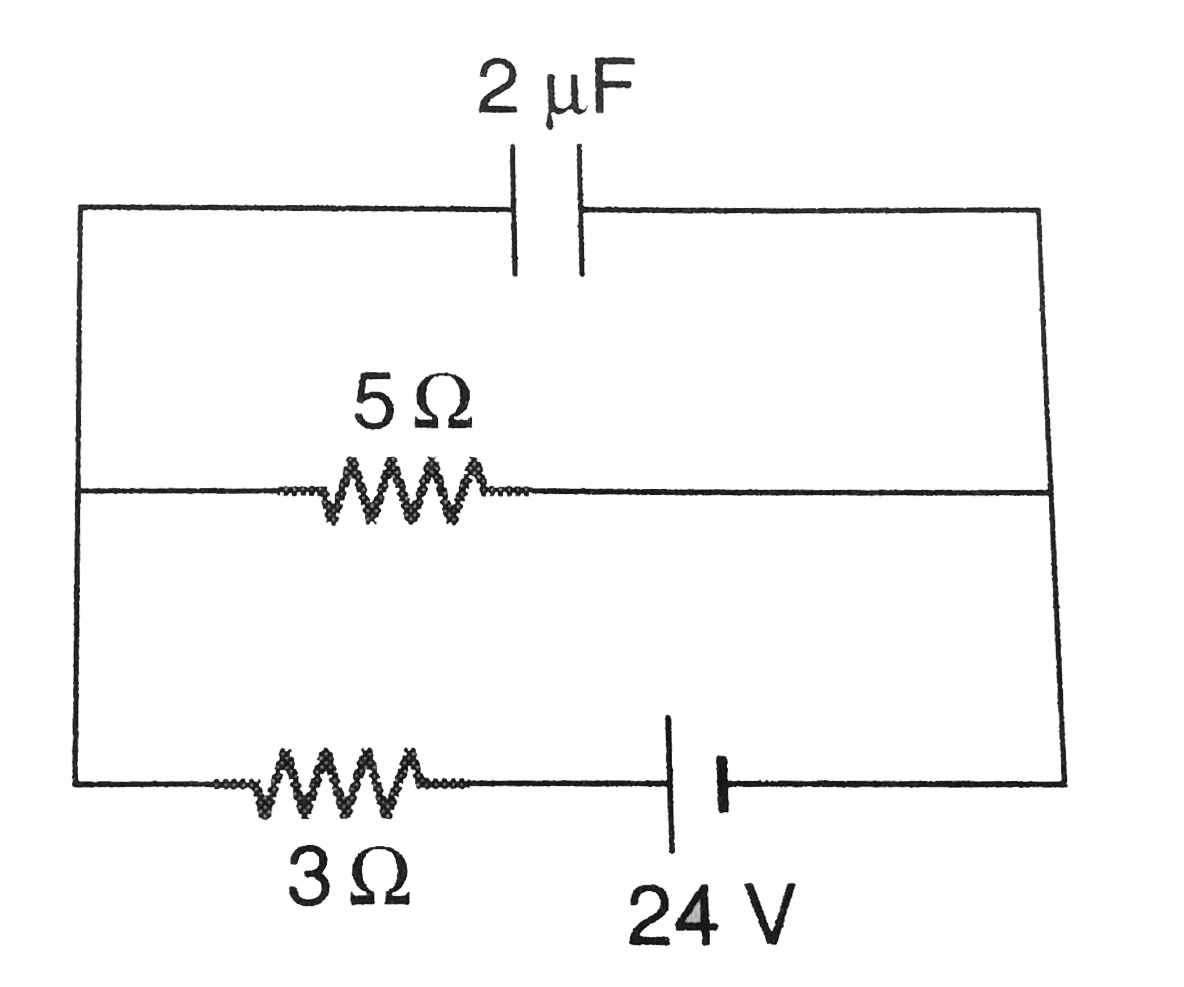 View Solution
View Solution