Determine the resistance RAB between points A abd B of the frame made of thin homogeneous wire (as shown in figure), assuming number of successively embedded equilateral tiangles ( with sides decreasing by half ) tends to infinity. Side AB is eual to a, and the resistance of unit length of the wire is ρ.
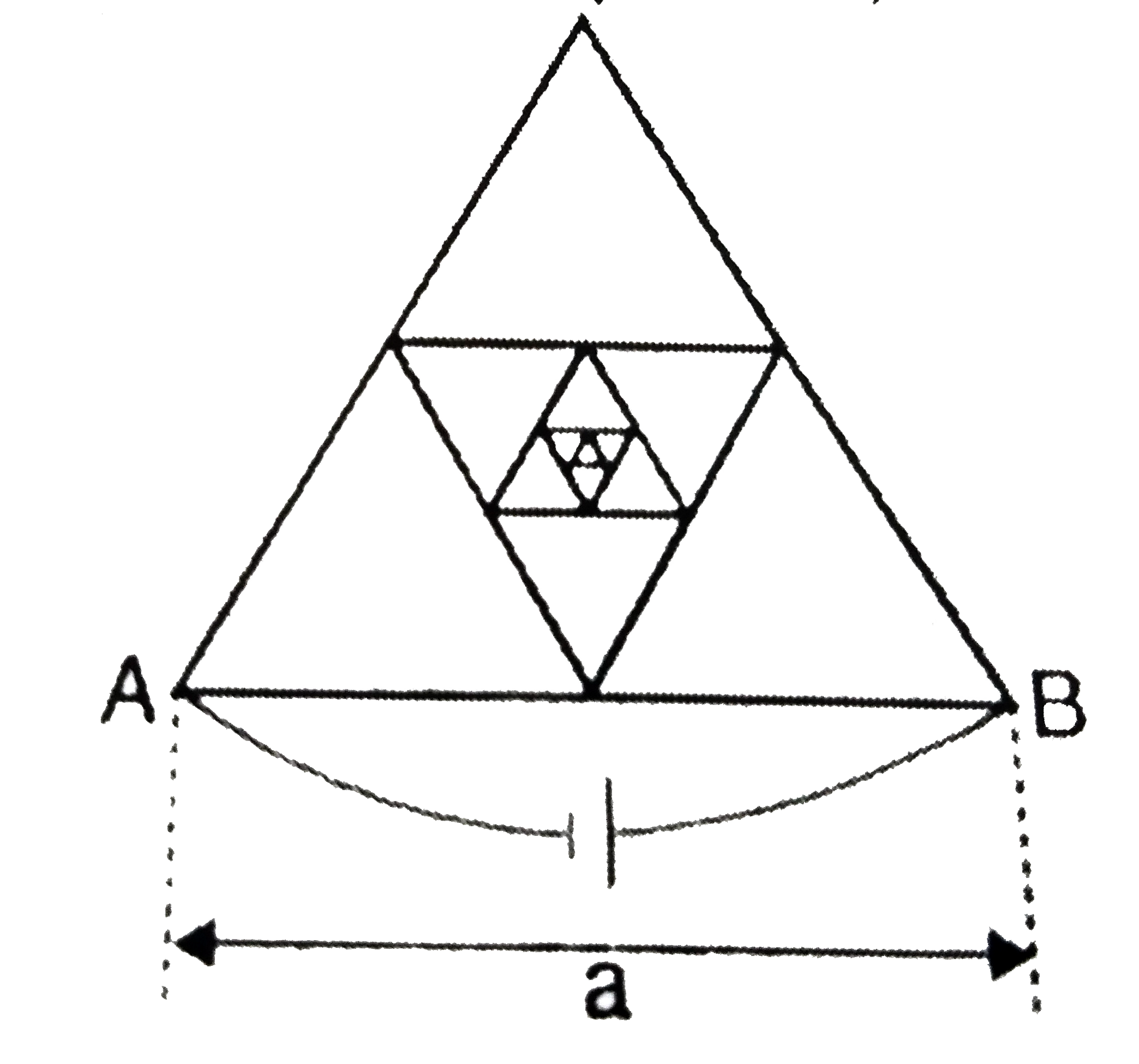
The correct Answer is:RAB=aρ(√7−1)3
Topper's Solved these Questions
Similar Questions
Find the resistacne RAB of the frame made of a thin wire. Assume that the number of successively embedded equilateral triangles (with sides decrasing ot half) tends to infifity Side AB is equal to a, and the resistance per unit length of wire is λ.
 View Solution
View SolutionFind the resistacne RAB of the frame made of a thin wire. Assume that the number of successively embedded equilateral triangles (with sides decrasing ot half) tends to infifity Side AB is equal to a, and the resistance per unit length of wire is λ.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
If an equilateral triangle is made of a uniform wire is resistance R, the equivalent resistance between the ends of sides is
A2R3BR3C2R9D9R2 - Question 2 - Select One
_2019_CBT3_E01_033_Q01.png)
A wire of length l and resistance R is bent in form of square form of square as shown in figure. If E is a mid point of side D,A, then equivalent resistance between points E& A is:A7R64B7R32C7R16D7R8 - Question 3 - Select One
A wire has linear resistance ρ (inΩm−1). Find the resistance R between points A and B if the side of the big square is d.
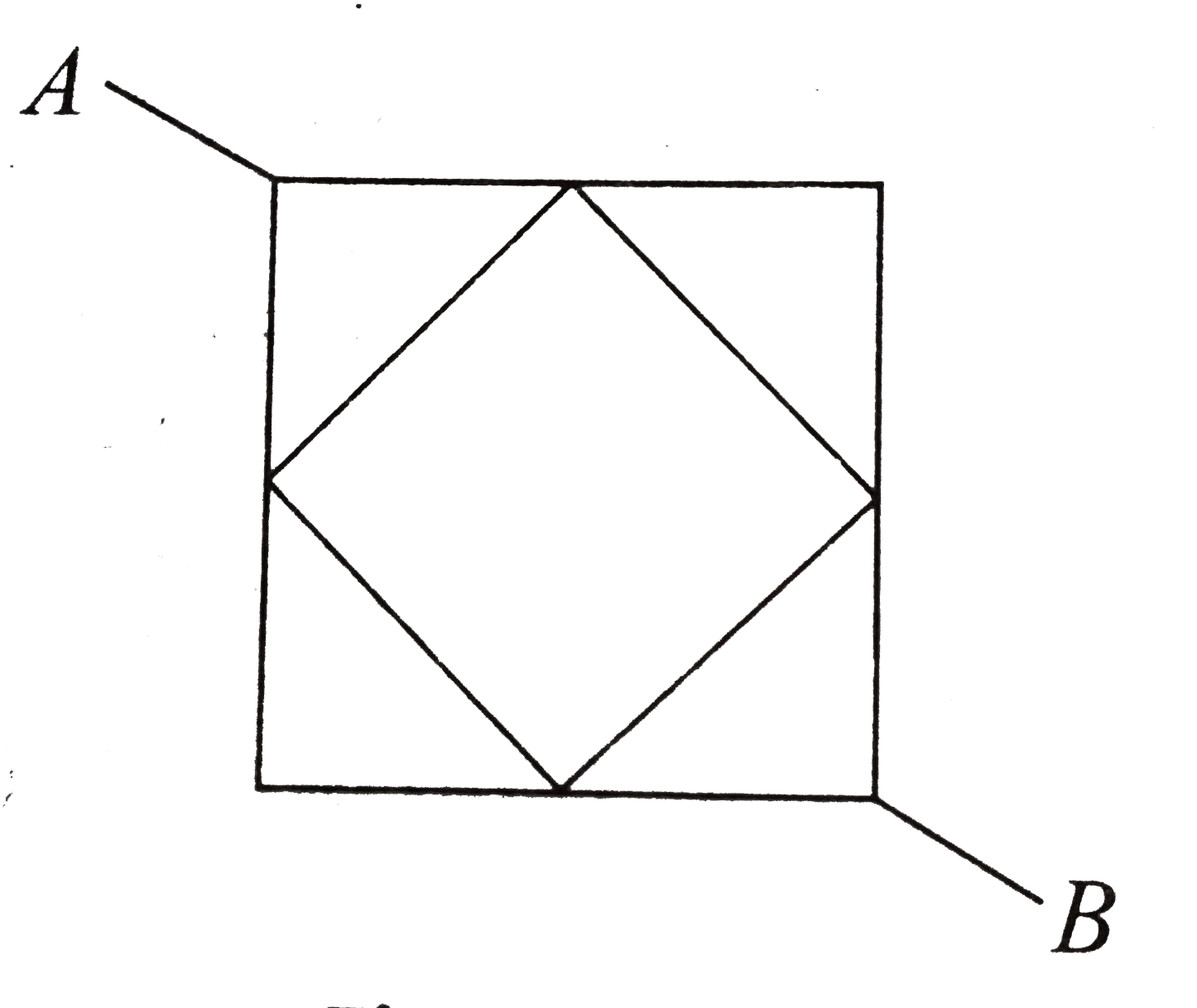 Aρd√2B(√2)ρdC2ρdDnone of these
Aρd√2B(√2)ρdC2ρdDnone of these
In the figure given below find the resistance between points A and B. Both the circle and the diatmeter are made of uniform wire of resistance rΩ per meter. The length AB is 2 metre.
 View Solution
View SolutionA wire has linear resistance ρ (inΩm−1). Find the resistance R between points A and B if the side of the big square is d.
 View Solution
View Solution
In the figure shown wire AB has a length of 100cm and resistance 8Ω. Find the balance point length l.View Solution
In the figure shown wire AB has a length of 100cm and resistance 8Ω. Find the balance point length l.View SolutionAs shown in the figure below, a cube is formed with ten identical resistance R (thick lines) and two shorteing wires (dotted lines) along the arms AC and BD
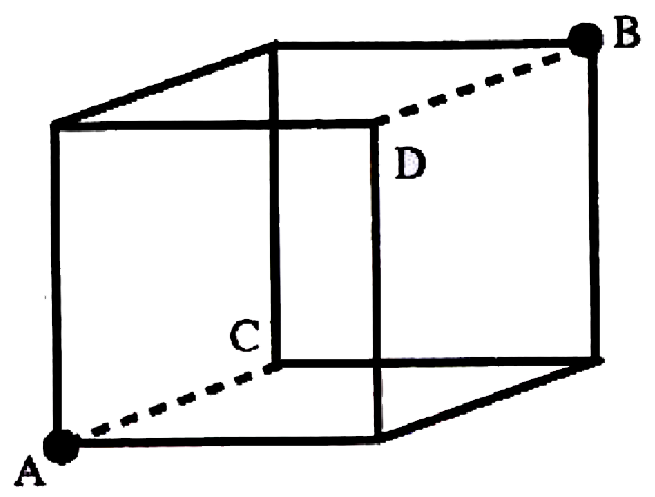
Resistance between point A and B is–View Solution

