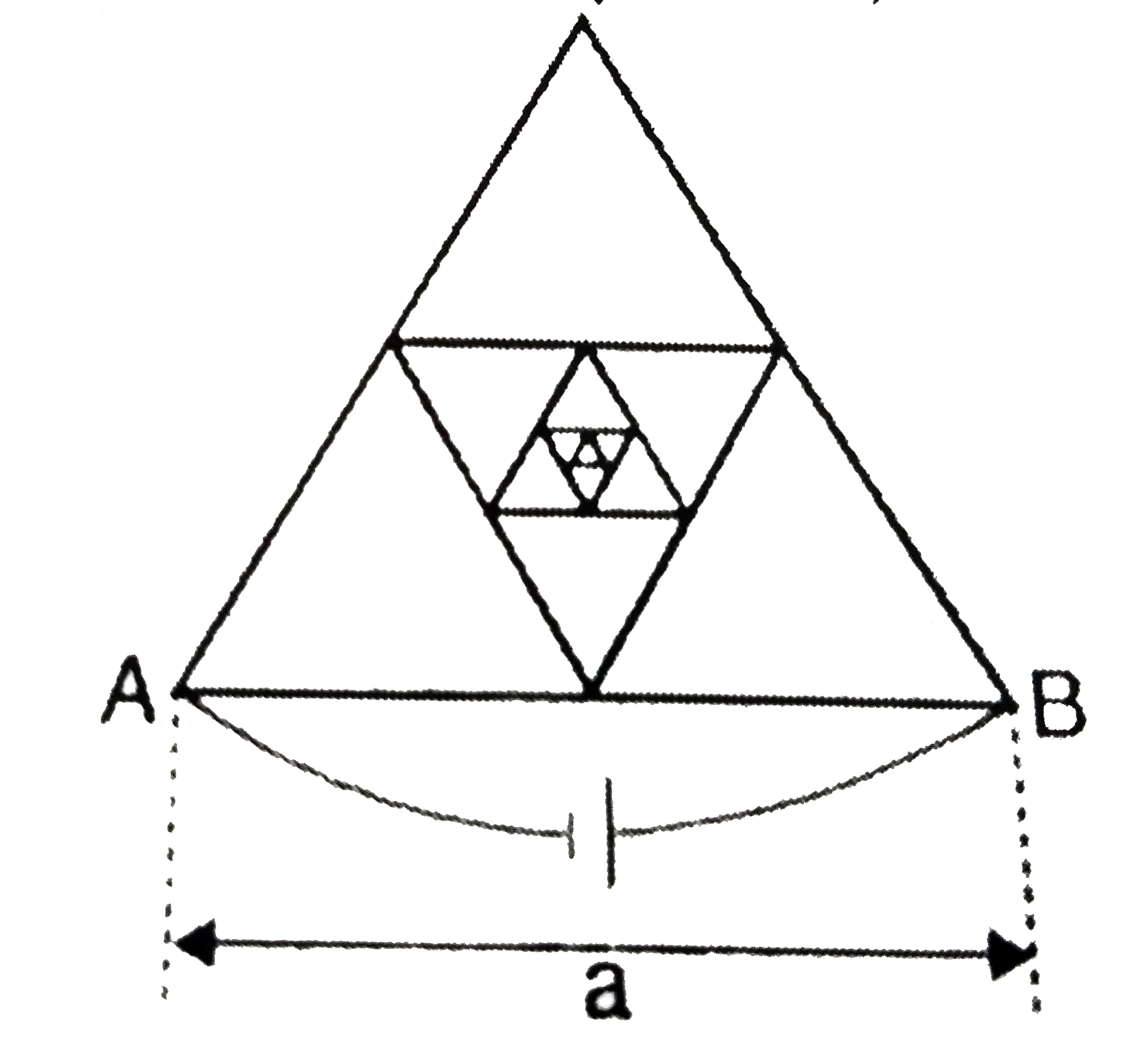
Find the resistacne RAB of the frame made of a thin wire. Assume that the number of successively embedded equilateral triangles (with sides decrasing ot half) tends to infifity Side AB is equal to a, and the resistance per unit length of wire is λ.

Let RAB=x be equivalent resistance of system between A and B. As the resistance of a conductor is directly proportional to length, the equivalnet resistance between A1 and B1 wil be x/2. Therefore, the equivalent circuit becomes as given in fig Effective resistance of 2r and x/2 is

R1=2xx22r+x2=2rx4r+x
Now R1 is in series with ∀1 and BB1, therefore, their effective
resistance is R2=R1+2r=2rx4r+x+2r
R2 is the parallel with 2r(of AB), so the net effective resistance
across AB is
x=R2×2rR2+2r=(2rx4r+x+2r)2r(2rx4r+x+2r)+2r
or 3x2+4rx−8r2=0 or x=−4r±√16r2+4×3×8r22×3
As x cannot be negative, we have
x=−4r+√16r2+96r26=(2√7−2)3r
But 2r=aλorr=aλ2, so
x=2(√7−1)3×a2λ=0.55aλ
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Single Correct72videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct16videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Exercise 5.250videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
Determine the resistance RAB between points A abd B of the frame made of thin homogeneous wire (as shown in figure), assuming number of successively embedded equilateral tiangles ( with sides decreasing by half ) tends to infinity. Side AB is eual to a, and the resistance of unit length of the wire is ρ.
 View Solution
View SolutionA wire of uniform cross section is used to make the given system. The radius of semicircle BCD is R and that of AFE is 2R while current I enters at point A.
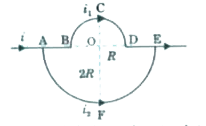
Find the magnetic field intensity at point O in the figure if resistance per unit length of wire is λ.View Solution
Knowledge Check
- Question 1 - Select One
If an equilateral triangle is made of a uniform wire is resistance R, the equivalent resistance between the ends of sides is
A2R3BR3C2R9D9R2 - Question 2 - Select One
A metal wire of resistance R is cut into three equal pieces that are then connected side by side to form a new wire, the length of which is equal to one third of the original length. The resistance of this new wire is:-
ARB3RCR9DR3 - Question 3 - Select One
A hemi-spherical network of radius a is made by using a conducting wire of resistance per unit length r. The equivalent resistance across OP is
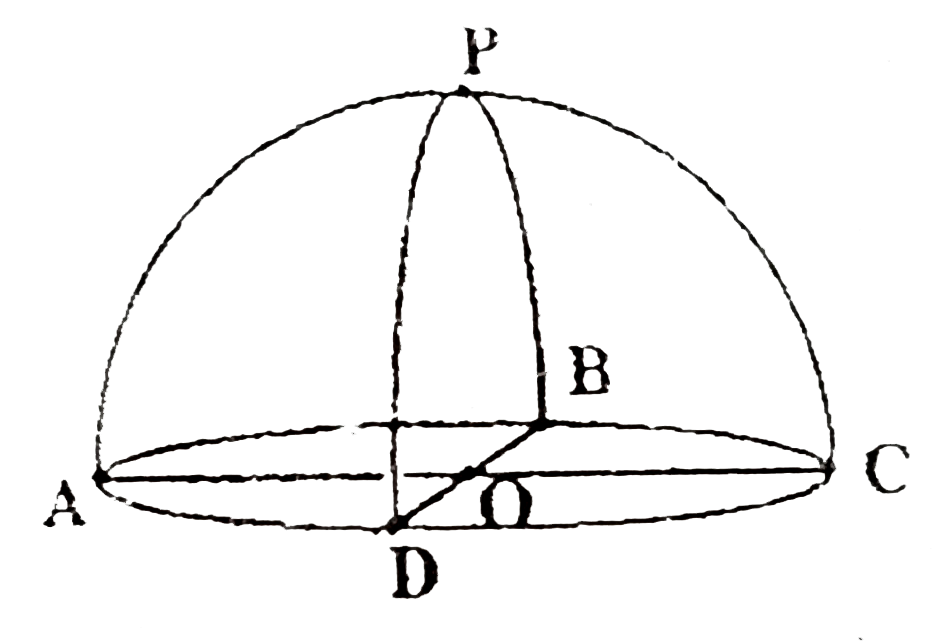 Ara(π+3)8Bra(π+2)8Cra(π+4)8Dra(π+1)8
Ara(π+3)8Bra(π+2)8Cra(π+4)8Dra(π+1)8
Two long parallel wires are located in a poorly conducting medium with respectivity ρ. The distance between the axes of the wires is equal to l, the cross -section radius of each wire equals a. In the case a<<l find,
(a) the current density at the point equally removed from the axes of the wire by a distance r if the potential difference between teh wires is equal to V,
(b) the electric resistances of the medium per unit length of the wires.View SolutionAdjacent figure represents an equilateral ΔABC of side length 2 units. Locus of vertex C as the side AB slides along the coordinate axes, is
View SolutionA hemispherical network of raidus a is made by using a conducting wire of resistance per unit length r. Find the equivalent resistance across OP.
 View Solution
View SolutionA copper wire is wire is wound on a wooden frame, whose shape is that of an equilateral triangle.If the number of turns of the coil per units length of the frame the same, then the self inductance of the coil:
View SolutionA long, horizontal wire AB rests on the surface of a table and carries a current I. Horizontal wire CD is vertically above wire AB, and is free to slide up and down on the two vetical mental guides C and D (as shown in Fig) Wire CD is connected through the sliding contacts to another wire that also carries a current I, opposite in direction to the current in wire AB. The mass per unit length of the wire CD is λ. To what euqilibrium heigth h will the wire CD rise, assuming that magnetic force on it is wholly due to the current in wire AB?
 View Solution
View Solution

