Figure shows tow concentric coplanar coils with radii a and b (a<<b). A current i=2t flows in the smaller loop. Neglecting self inductance of larger loop

(a) Find the mutual inductance of two coils.
(b) Find the emf induced in the larger coil
(c) If the resistance of the larger loop is R find the current in it as a function of time.
(a) To find mutual inductance , it does not matter in which coil we consider current and in which flux is calculated (Reciprocity theorem) Let current i be flowing in the larger coil. Magnetic field at the centre =μ0i2b.
flux through the smaller coil =μ0i2bπa2 ∴M=μ02bπa2
(b) |emf induced in larger coil|=m[(didt) in smaller coil]=μ02bπa2(2)=μ0πa2b
(c) current in the larger coil =μ0πa2bR.
Similar Questions
Figure. shows two concentric coplanar coils with radii a and b(a<<b). A current I=2t flows in the smaller loop. Neglecting self-inductance of the larger loop,
a. find the mutual inductance of the two coils,
b. find the emf induced in the larger coil,
c. if the resistance of the larger loop is R, find the current in it as a function of time.

View SolutionFigure shows two concentric loops of radii R and r (R gtgt r). A current i is passed through the outer loop. Find the flux linked with inner loop and the mutual inductance of the arrangement.
View Solution
Knowledge Check
Two concentric co - planar circular loops of radius R and r(<<R) are placed as shown in the figure. The mutual inductance of the system will be
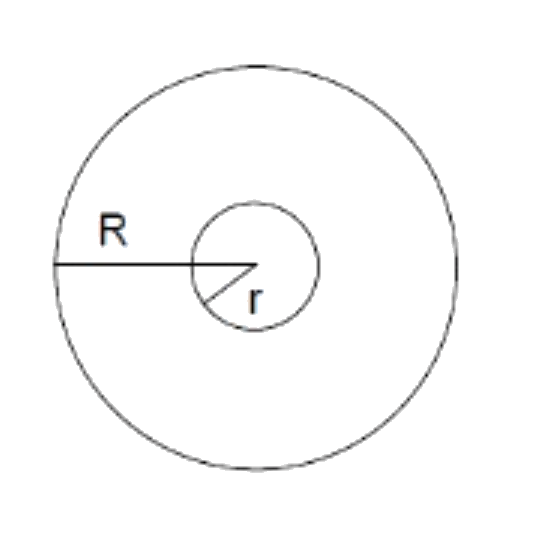 Aπμ0r22RBπμ0r24RCπμ0R24rDπμ0R22r
Aπμ0r22RBπμ0r24RCπμ0R24rDπμ0R22rIf the rate of change of current is 1A per second in one coil induces an emf of 2 V in the neighbouring coil, the mutual inductance of two coils is
A2 HB1.5 HC1 HD2.5 HThe coefficient of mutual inductance of two coils is 10 mH. IF the current flowing in one coil is 4A then the induced e.m.f in the second coil will be
A40 mVB20 mVCzeroD10 mV
Find the mutual inductance between two rectangular loops, shown in the figure.
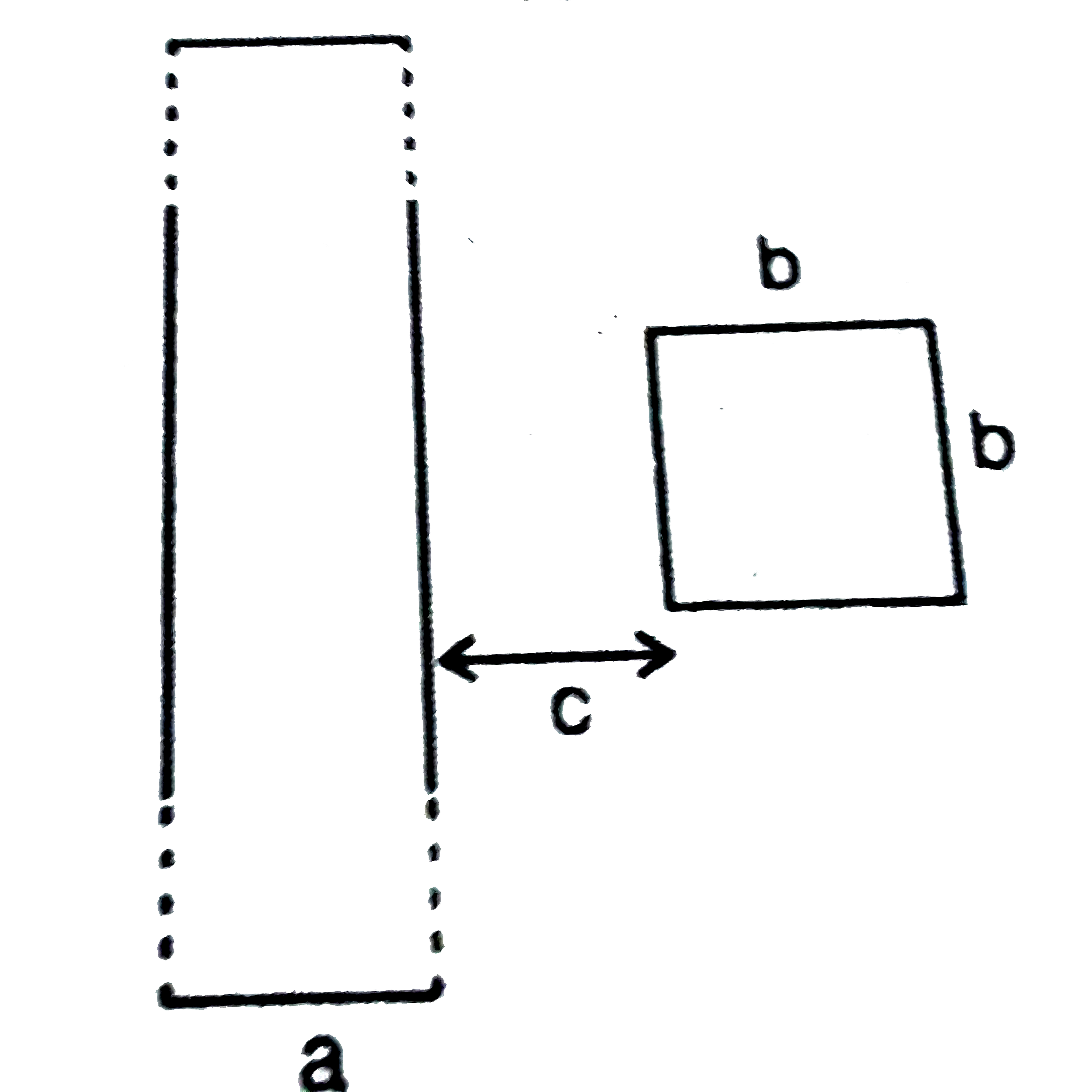
View SolutionFind the mutual inductance between the circular coil and the loop shown in figure.
View SolutionFind the mutual inductance of two concentric coils of radii a1 and a2(a1<<a2) if the planes of the coils are same.

View SolutionA constant current I flows through a long straight wire as shown in figure. A square loop starts moving towards righ with as constant speed v.

a Find induced emf produced i the loop as a function x
b. If total resistance of the loop is R, then find induced current in the loop,
View SolutionMutual induction is the produced of induced emf in a coil due to the change of current in the
View Solution
