Calculate electric field at a point on axis, which at a distance x from centre of uniformly charged disc having surface charge density σ and R which also contains a concentric hole of radius r.
Consider a ring of radius y(r<y<R) and width dy concentric with disc and in the plane of the disc. Due to this ring , the electric field at the point P :

dE=K(dq)x[X2+Y2]3/2
Enet=R∫rKx.σ(2πy)dy[x2+y2]3/2 [∵=σ2πydy]
Enet=2πσkx2x2+R2∫x2+r2dtt3/2, put x2+y2=t,2y.dy=dt
=σx2ε0[1√x2+r2−1√x2+R2] away from centre
Alternate method
We can use superposition principle to solve this problem.
(i) Assume a disc without hole of radius R having surface charge density +σ
(ii) Also assume a concentric disc of radius r in the same plane of first disc having charge density −σ, Now using derived formula in last example the net electric field at the centre is :
−−→Enet=−→ER+−→Er=σx2ε0[1√r2+x2−1√R2+x2] away from centre.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Derive the expression of electric field intensity at a point 'P' which is situated at a distance x on the axis of uniformly charges disc of radius R and surface charge density σ. Also, derive results for
(i) x>>R (ii) x<<R
View SolutionElectric field at the centre of uniformly charge hemispherical shell of surface charge density σ is σnε0 then find the value of n.

View Solution
Knowledge Check
Electric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
Ar−1BrCr2Dr−2The electric field intensity in free space at a distance 'r' outside a charged conducting sphere of radius 'R' in terms of surface charge density σ is
Aσε0[Rr]2Bε0σ[Rr]2CRr[σε0]2DRσ[rε0]2Calculate the magnetic field at distance y from the centre of the axis of a disc of radius r and unifrom surface charge density σ, If the disc spins with angular velocity ω ?
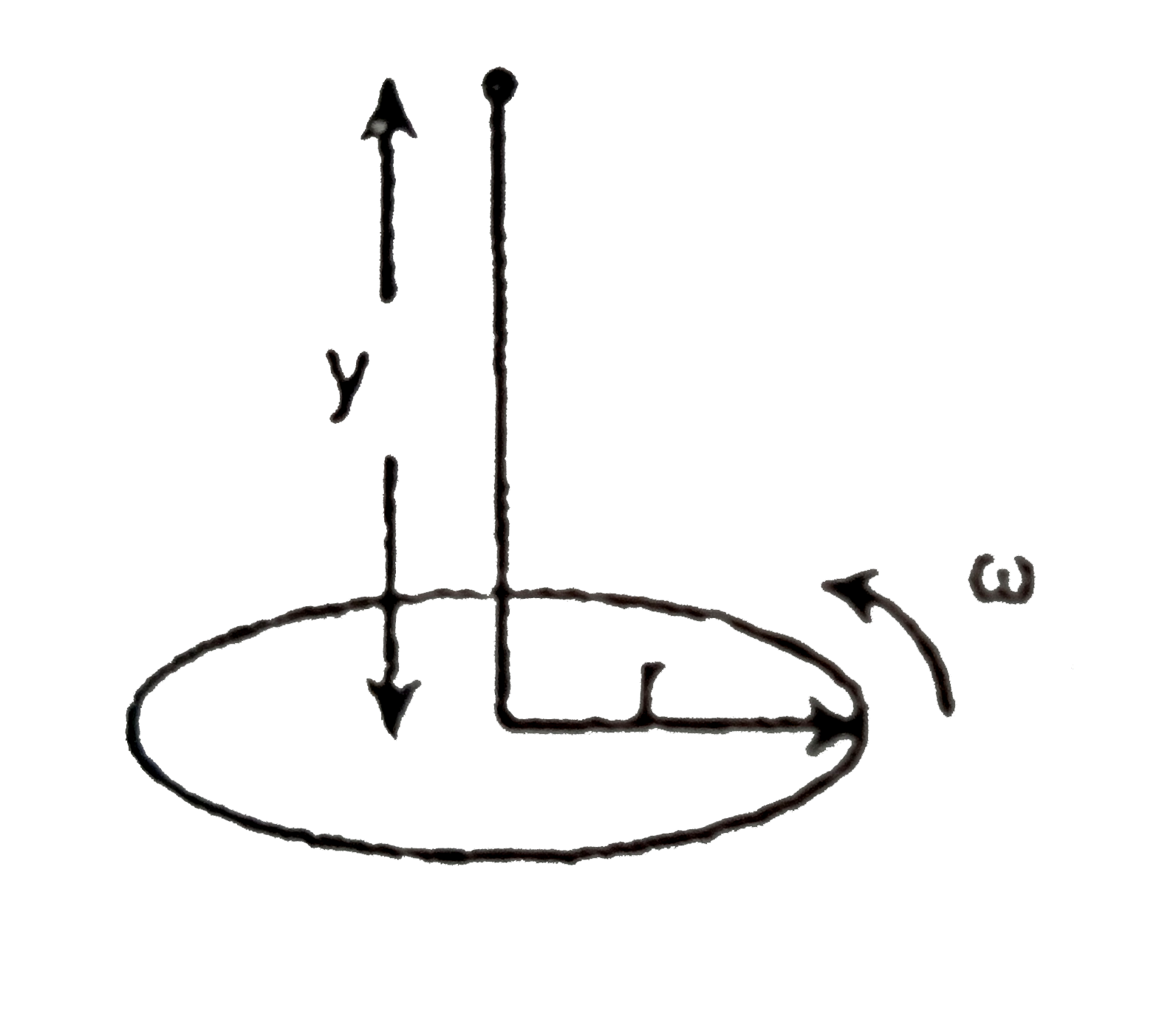 Aμ0σω3(r2−2y2√r2−y2+2y)Bμ0σω2(r2+2y2√r2+y2)Cμ0σω2(r2+2y2√r2+y2−2y)D2μ0σω3(r2+2y2√r2+y2−2y)
Aμ0σω3(r2−2y2√r2−y2+2y)Bμ0σω2(r2+2y2√r2+y2)Cμ0σω2(r2+2y2√r2+y2−2y)D2μ0σω3(r2+2y2√r2+y2−2y)
Calculate gravitational field intensity at a distance x on the axis from centre of a uniform disc of mass M and radius R .
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View SolutionA thin copper ring of radius a is charged with q units of electricity. Calculate the electric field at a point at a distance x from the centre and on the axis of the ring. Use the result to find the electirc field due to a charged disc of surface density of charge ε.
View SolutionThe magnitude of an electric intensity at a point which is at a distance 'r' from the centre of a charged spherical conductor of radius 'R' in terms of the surface charge density 'σ' is given by 'E' where
View SolutionThe electric field intensity in free space at a distance 'r' outside a charged conducting sphere of radius 'R' in terms of surface charge density σ is
View Solution
