Find out energy stored inside a solid non-conducting sphere of total charge Q and radius R. [Assume charge is uniformly distributed in its volume.]
We can charge solid sphere to be made of large number of concentric spherical shells. Also electric field intensity at the location of any particular shell is constant.
∴Uinside=∫R012ε0E2dV
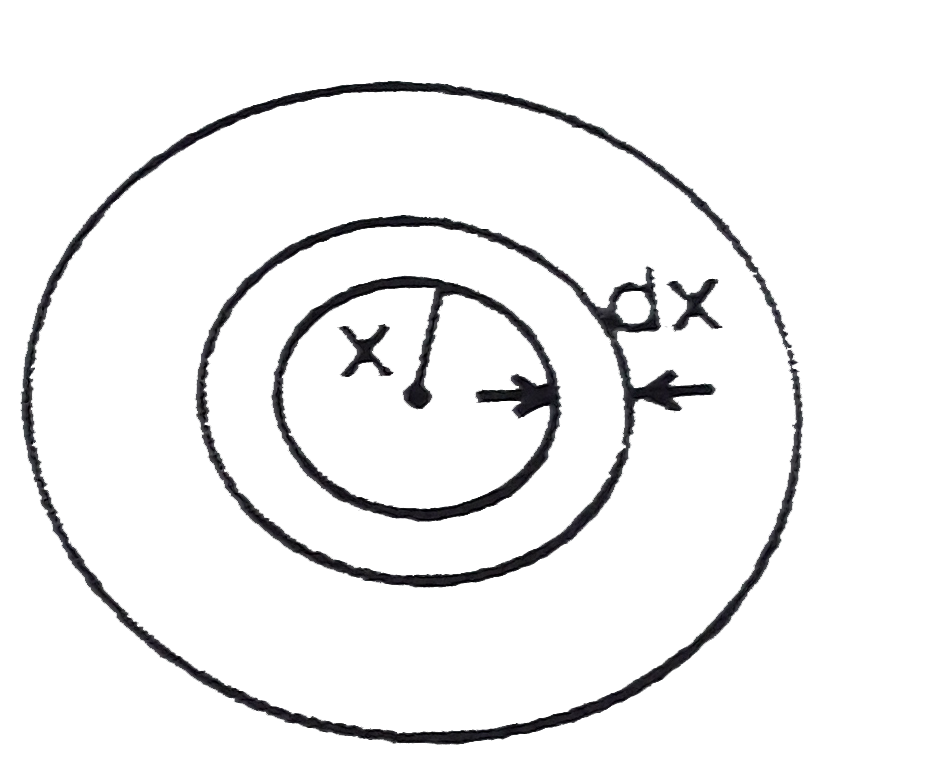
Consider an elementary shell of thickness dx and radius x.
Volume of the shell =(4πx2dx)
Uinside=∫R012ε0[KQxR3]2.4πx2dx=12ε0K2Q24πR6∫R0x4dx
=4πε02R6Q2(4πε0)2.R55=Q240πε0R=KQ210R.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Problems22videos
ELECTROSTATICS
- BOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)9videos
ELECTROSTATICS
- BOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P19videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II10videos
EXPERIMENTAL PHYSICS
Similar Questions
Find out energy stored in the electric field of uniformly charged thin spherical shell of total charge Q and radius R.
View SolutionFigure shows a uniformly charged thin non-conducting sphere of total charge Q and radius R. If point charge q is situated at point 'A' which is at a distance r<R from centre of the sphere, then find out following :
(i) Force acting on charge q.
(ii) Electric field at centre of sphere.
(iii) Electric field at point B.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A solid conducting sphere of radius r is given some charge. Then :
AThe charge is uniformly distributed over its surface, if there is an external electric field.BDistribution of charge over its surface will be non uniform if no external electric field exist in spaceCElectric field strength inside the sphere will be equal to zero only when no external electric field existsDPotential at every point of the sphere must be same in all cases - Question 2 - Select One or More
There is a solid non-conducting sphere of radius R. Sphere is uniformly charged over the volume. Electric field due to this where in observed.
AElectric field intensity at the centre of sphere can never be non-zero.BMagnitude of electric field intensity at a point inside the sphere is directly proportional to the distance of the point from centre of sphere.CMagnitude of electric field intensity is directly proportional to 1r2 for points outside the sphere where r is the distance of point from the centre of sphereDMagnitude of electric field intensity at any point is less than its magnitude on sphere's surface. - Question 3 - Select One
A uniform charged shell is reassembled in the form of a sphere of same radius but charge uniformly distributed through out of its volume. Find the ratio of initial potential energy to work required for it.
A2B3C5D6
An isolated non-conducting solid sphere of radius R is given an electric charge. The charge is uniformly distributed in the volume of sphere. The graph which shows the correct variation of magnitude of electric field with distance from the centre of the sphere is
View SolutionA solid uniformly charged ficed non-conducting sphere of total charge Q and radius R contains a tunnel of negligible diameter. If a point charge '-q' of mass 'm' is released at rest from point P as shown in figure then find out its velocity at following points

(i) At the surface of sphere
(ii) At the centre of the sphereView SolutionFind out electric field intensity due to uniformly charged solid non-conducting sphere of volume charge density ρ and radius R at following points :
(i) At a distance r from surface of sphere (inside)
(ii) At a distance r from the surface of sphere (outside)View SolutionA charge Q is uniformly distributed inside a non- conducting sphere of radius R. Find the electric potential energy stored in the system.
View SolutionFind the energy stored in the electirc field produced by a metal sphere of radius R containing a charge Q.
View Solution

