A charge particle q1, is at position (2, -1, 3). The electrostatic force on another charged particle q2 at (0, 0, 0) is :
q1q256π∈0(2ˆi−ˆj+3ˆk)
q1q256√14π∈0(2ˆi−ˆj+3ˆk)
q1q256π∈0(ˆj−2ˆi−3ˆk)
q1q256√14π∈0(ˆj−2ˆi−3ˆk)
The correct Answer is:D
To find the electrostatic force on a charged particle q2 located at the origin (0, 0, 0) due to another charged particle q1 located at (2, -1, 3), we can follow these steps:
Step 1: Identify the positions of the charges
- The position of charge q1 is given as r1=(2,−1,3).
- The position of charge q2 is given as r2=(0,0,0).
Step 2: Calculate the displacement vector r from q1 to q2
The displacement vector r is calculated as:
r=r2−r1=(0,0,0)−(2,−1,3)=(−2,1,−3)
Step 3: Calculate the magnitude of the displacement vector r
The magnitude r is given by:
r=√(−2)2+(1)2+(−3)2=√4+1+9=√14
Step 4: Calculate the unit vector ^r
The unit vector ^r in the direction of r is:
^r=rr=(−2,1,−3)√14=(−2√14,1√14,−3√14)
Step 5: Use Coulomb's Law to find the force F
Coulomb's Law states that the electrostatic force F between two point charges is given by:
F=kq1q2r2^r
where k=14πϵ0.
Substituting the values:
F=kq1q2(√14)2^r=kq1q214^r
Step 6: Substitute ^r into the force equation
F=kq1q214(−2√14,1√14,−3√14)
This can be simplified to:
F=kq1q214√14(−2,1,−3)
Final Result
Thus, the electrostatic force on charge q2 due to charge q1 is:
F=kq1q214√14(−2,1,−3)
- The position of charge q1 is given as r1=(2,−1,3).
- The position of charge q2 is given as r2=(0,0,0).
The displacement vector r is calculated as:
r=r2−r1=(0,0,0)−(2,−1,3)=(−2,1,−3)
The magnitude r is given by:
r=√(−2)2+(1)2+(−3)2=√4+1+9=√14
The unit vector ^r in the direction of r is:
^r=rr=(−2,1,−3)√14=(−2√14,1√14,−3√14)
Coulomb's Law states that the electrostatic force F between two point charges is given by:
F=kq1q2r2^r
where k=14πϵ0.
F=kq1q2(√14)2^r=kq1q214^r
F=kq1q214(−2√14,1√14,−3√14)
This can be simplified to:
F=kq1q214√14(−2,1,−3)
Thus, the electrostatic force on charge q2 due to charge q1 is:
F=kq1q214√14(−2,1,−3)
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Part - II Section (B)
9 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Part - II Section (C)
14 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (J)
7 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Three particles are fixed on an x axis. Particle 1 of charge q1 is at x = -a, and particle 2 charge q2 is at x = +a. If their net electrostatic force on particle 3 of charge +Q is to be zero, what must be the ratio q1/q2 when particle 3 is at (a) x = +0.750 a and (b) x = +1.50 a ?
View SolutionIn Fig. four particles form a square. The charges are q1=q4=Q and q2=q3=q. (a) What is Q/q is the net electrostatic force on particles 2 and 3 is zero ? (b) Is there any value of q makes the net electrostatic force on each of the four particles zero ? Explain.

View Solution
Knowledge Check
In the above question, the ratio of masses of the charge particles q1,q2,andq3 is
A1:1:1Bq1:q2:q3C1:√3:2DThis ratio cannot be calculated
A charged particle of mass m1 and charge q1 is revolving in a circle of radius r .Another charged particle of charge q2 and mass m2 is situated at the centre of the circle.If the velocity and time period of the revolving particle be v and T respectively then
View SolutionIn Fig., three charged particles lie on an x axis. Particles 1 and 2 are fixed in place. Particle 3 is free to move, but the net electrostatic force on it from particles 1 and 2 happens to be zero. If 2.0L23=L12, what is the ratio q1/q2 ?
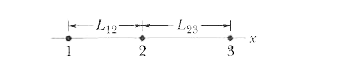
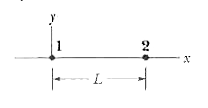
View SolutionIn Fig., particle 1 of charge +6.0μC and particle 2 of charge −2.0μC are held at separation L=10.0cm on an x axis. If particle 3 of unknown charge q3 is to be located such that the net electrostatic force on it from particles 1 and 2 is zero, what must be the (a) x and (b) y coordinates of particle 3 ?
View SolutionInside a neutral hollow conducting sphere of radius X and centre C, a point charge q is placed as shown in the figure. Another point charge q1, is placed outside the sphere at distance d from centre. The net- electrostatic force on charge q placed at the centre is K=14πε0

View SolutionThe charges and coordinates of two charged particles held fixed in an xy plane are q1=+3.0μC,x1=3.5cm,y1=0.50cm, and q2=−4.0μC,x2=−2.0cm,y2=1.5cm. Find the (a) magnitude and (b) direction of the electrostatic force on particle 1 due to particle 2. At what (c ) x and (d) y coordinates should a third particle of charge q3=+6.0μC be placed such that the net electrostatic force on particle 1 due to particles 2 and 3 is zero ?
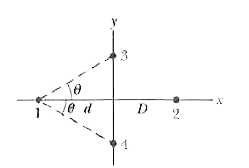
View SolutionFigure shows an arrangement of four charged particles, with angle θ=35.0∘ and distance d = 2.00 cm. Particle 2 has charge q2=+8.00×10−19C, particle 3 and 4 have charges q3=q4=−1.60×10−19C, (a) What is distance D between the origin and particle 2 if the net electrostatic force on particle 1 due to the other particles is zero ? (b) If particles 3 and 4 were moved closer to the x axis but maintained their symmetry about that axis, would the required value of D be greater than, less than, or the same as the part (a) ?
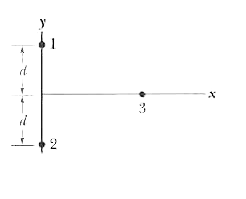
View SolutionIn Fig., particles 1 and 2 of charge q1=q2=+4e are on a y axis at distance d = 1.70 m from the origin. Particle 3 of charge q3=+8e is moved gradually along the x axis from x = 0 to x = +5.0 m. At what values of x will the magnitude of the electrostatic force on the third particle from the other two particles be (a) minimum and (b) maximum ? What are the (c ) minimum and (d) maximum magnitudes ?
View Solution
