A particle of mass 2 g and charge 1μC is held at rest on a frictionless surface at a distance of 1m from a fixed charge of 1 mC. If the particle is released it will be repelled. The speed of the particle when it is at distance of 10 m from fixed charge is :
100 m/s
90 m/s
60 m/s
45 m/s
The correct Answer is:B
To solve the problem step by step, we will use the principle of conservation of energy, specifically the relationship between kinetic energy and electrostatic potential energy.
Step 1: Understand the Given Data
- Mass of the particle, m=2g=2×10−3kg
- Charge of the particle, q1=1μC=1×10−6C
- Fixed charge, q2=1mC=1×10−3C
- Initial distance from the fixed charge, r1=1m
- Final distance from the fixed charge, r2=10m
Step 2: Write the Energy Conservation Equation
When the particle is released, the change in kinetic energy of the particle equals the change in electrostatic potential energy:
ΔKE=ΔPE
This can be expressed as:
12mv2−0=Uf−Ui
where Uf is the potential energy at r2 and Ui is the potential energy at r1.
Step 3: Calculate the Initial and Final Potential Energy
The electrostatic potential energy U between two point charges is given by:
U=kq1q2r
where k is Coulomb's constant, k=9×109N m2/C2.
1. Initial Potential Energy Ui at r1=1m:
Ui=kq1q2r1=9×109⋅(1×10−6)(1×10−3)1=9×109⋅1×10−9=9J
2. Final Potential Energy Uf at r2=10m:
Uf=kq1q2r2=9×109⋅(1×10−6)(1×10−3)10=9×109⋅1×10−10=0.9J
Step 4: Substitute into the Energy Equation
Substituting Ui and Uf into the energy equation:
12mv2=Uf−Ui
12mv2=0.9−9=−8.1J
This indicates a mistake, as potential energy should decrease, thus:
ΔPE=Ui−Uf=9−0.9=8.1J
So,
12mv2=8.1
Step 5: Solve for Velocity v
Rearranging the equation to solve for v:
v2=2⋅8.1m
Substituting m=2×10−3kg:
v2=16.22×10−3=8100
v=√8100=90m/s
Final Answer
The speed of the particle when it is at a distance of 10 m from the fixed charge is 90m/s.
- Mass of the particle, m=2g=2×10−3kg
- Charge of the particle, q1=1μC=1×10−6C
- Fixed charge, q2=1mC=1×10−3C
- Initial distance from the fixed charge, r1=1m
- Final distance from the fixed charge, r2=10m
When the particle is released, the change in kinetic energy of the particle equals the change in electrostatic potential energy:
ΔKE=ΔPE
This can be expressed as:
12mv2−0=Uf−Ui
where Uf is the potential energy at r2 and Ui is the potential energy at r1.
The electrostatic potential energy U between two point charges is given by:
U=kq1q2r
where k is Coulomb's constant, k=9×109N m2/C2.
Ui=kq1q2r1=9×109⋅(1×10−6)(1×10−3)1=9×109⋅1×10−9=9J
Uf=kq1q2r2=9×109⋅(1×10−6)(1×10−3)10=9×109⋅1×10−10=0.9J
Substituting Ui and Uf into the energy equation:
12mv2=Uf−Ui
12mv2=0.9−9=−8.1J
This indicates a mistake, as potential energy should decrease, thus:
ΔPE=Ui−Uf=9−0.9=8.1J
So,
12mv2=8.1
Rearranging the equation to solve for v:
v2=2⋅8.1m
Substituting m=2×10−3kg:
v2=16.22×10−3=8100
v=√8100=90m/s
The speed of the particle when it is at a distance of 10 m from the fixed charge is 90m/s.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Part - II Section (E)
2 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Part - II Section (F)
2 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Part - II Section (C)
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
A particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View SolutionA particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View Solution
Knowledge Check
A charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2t22mCEq2m2t2DEqm2tA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
Aq2EyBqEyCaE2yDqEy2A charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2r22mCEq2m2t2DEqm2t
A charged particle of mass m and charge q is kept initially at rest on a frictionless surface. Another charged particle of mass 4m and charge 2q starts moving with velocity v towards it. Calculate the distance of the closest approach for both the charged particles.
View SolutionTwo identical charges, 5μC each are fixed at a distance 8 cm and a charged particle of mass 9×10−6kg and charge −10μC is placed at a distance 5 cm from each of them and is released. Find the speed of the particle when it is nearest to the two charges.
View SolutionA wedge of mass M lies on a smooth fixed wedge of inclination θ. A particle of mass m lies on the wedge of mass M in the figure. All surfaces are frictionless and the distance of the block from the fixed wedge is l. Find.
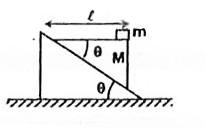
(a) Normal reaction between m and M
(b) the time after which the particle will hit the fixed plane.
View SolutionFour particles, each of mass m and charge q, are held at the vertices of a square of side 'a'. They are released at t = 0 and move under mutual repulsive forces speed of any particle when its distance from the centre of square doubles is
View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View Solution
