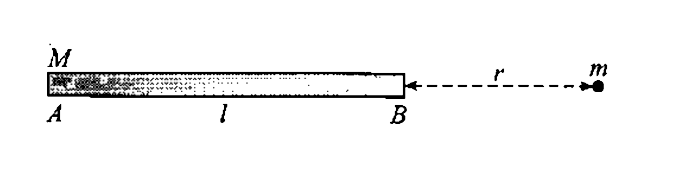
Calculate the force exerted by point mass m on rod of uniformly distributed mass M and length l (Placed as shown in figure)
 .
.
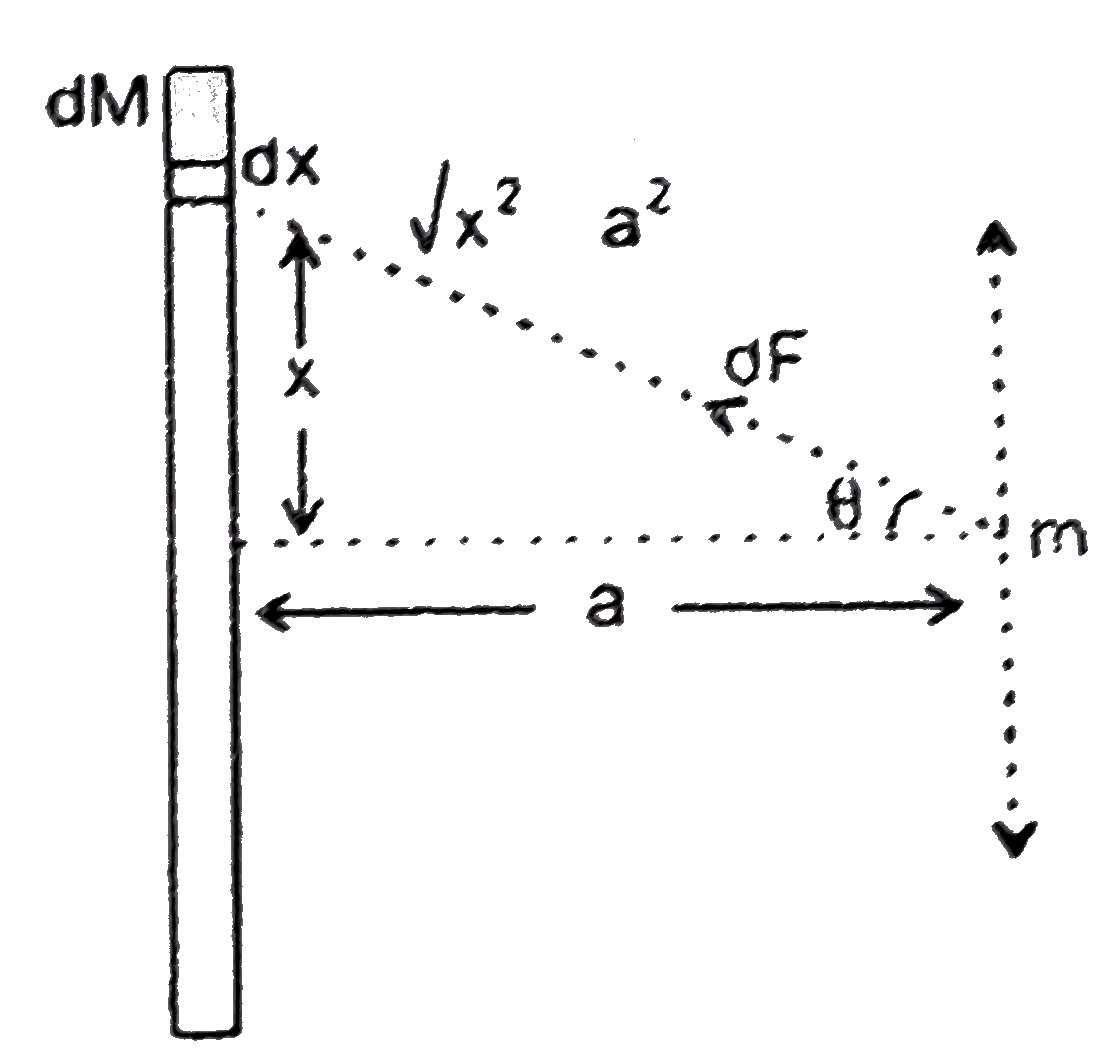
∵ Direction of force is changing at every element. We have to make components of force and then integrate.
Net vertical force =0
dF = force element =G.dM.m(x2+a2)
dFh=dFcosθ = Force on element in horizontal direction =G.dM.m(x2+a2)cosθ
∴Fh=∫G.M.mcosθdxl(x2+a2)=G.M.mll/2∫−l/2cosθ.dx(x2+a2)=GMmla2l/2∫−l/2cosθ.dxsec2θ
where x=a than θ then dx=asec2θdθ
=GMmla[sinθ]l/2l/2tanθ=xa,thesinθ=x√x2+a2
=GMmla[x√x2+a2]l/2−l/2=√GMmlla√l24+a2=GMma√(l24+a2)
 .
.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - EXAMPLE2videos
GRAVITATION
- BOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - EXERCISE-1 PART-113videos
GRAVITATION
- BOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - HIGH LEVEL PROBLEMS16videos
GRAVITATION
- BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems35videos
GEOMATRICAL OPTICS
- BOOK - RESONANCECHAPTER - NUCLEAR PHYSICSEXERCISE - Advanced level solutions16videos
NUCLEAR PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The gravitational force of attraction between a uniform sphere of mass M and a uniform rod of length l and mass in as shown in figure is
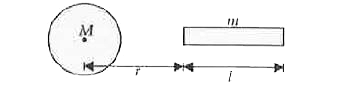 AGMmr(r+1)BGMr2CMm2D(r2+1)mM
AGMmr(r+1)BGMr2CMm2D(r2+1)mM - Question 2 - Select One
Charge Q is uniformly distributed on a dielectric rod AB of length 2l. The potential at P shown in the figure is equal to
 AQ4πε0(2l)BQ4πε0(l)ln2CQ4πε0(2l)ln3DNone of these
AQ4πε0(2l)BQ4πε0(l)ln2CQ4πε0(2l)ln3DNone of these
Find the gravitational potential energy of system consisting of uniform rod AB of mass M, length l and a point mass m as shown in figure.
 View Solution
View SolutionThe gravitational force between earth of radius R and mass M and rod of length R and mass m placed as shown in the figure is 12GMm. Find the value of n.
 View Solution
View SolutionCalculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.
 View Solution
View SolutionCalculate the potential due to a thin uniformly charged rod of length L at the poiot P shown in figure. The lioear charge density of the rod is λC/m
 View Solution
View SolutionShow that the centre of mass of uniform rod of mass M and length L lies at the middle point of the rod.
View SolutionAs shown in the figure, two blocks, each of mass m, suspended from the ends of a rigid light rod of length L. The rod is held horizontally on the fulcrum and then released.
(a) Find the initial angular acceleration of the rod.
(b) If the mass of rod is also m uniformly distributed. find the tension in the strings attached to blocks.
 View Solution
View Solution