Four similar particles of mass m are orbiting in a circle of radius r in the same direction and same speed because of their mutual gravitational attractive force as shown in the figure . Speed of a particle is given by
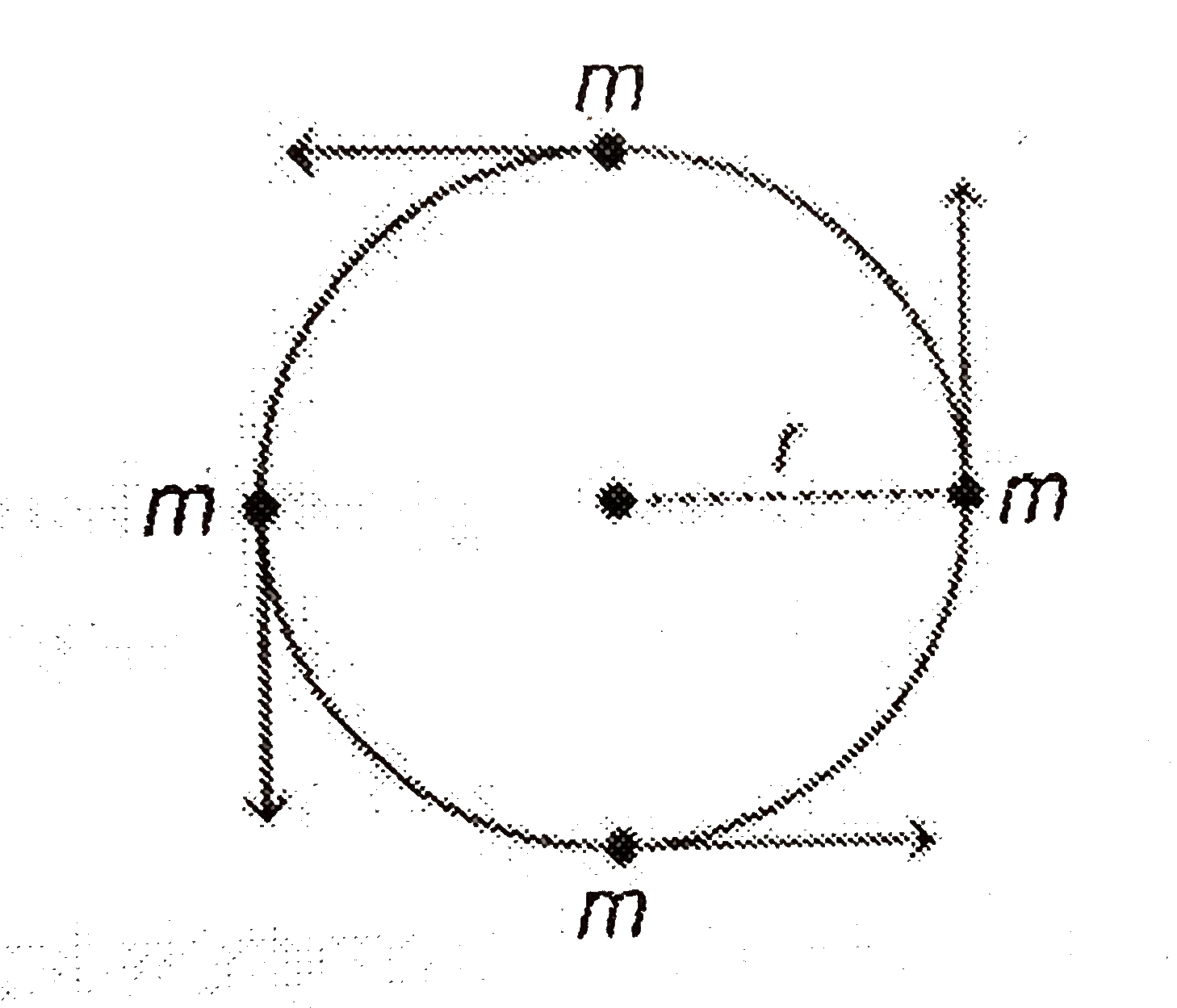
[Gmr(1+2√24)]12
3√GMr
√Gmr(1+2√2)
zero
The correct Answer is:A
Step by step video, text & image solution for Four similar particles of mass m are orbiting in a circle of radius r in the same direction and same speed because of their mutual gravitational attractive force as shown in the figure . Speed of a particle is given by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - EXERCISE-1 PART-32videos
GRAVITATION
- BOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - EXERCISE-2 PART-116videos
GRAVITATION
- BOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - EXERCISE-1 PART-113videos
GRAVITATION
- BOOK - RESONANCECHAPTER - GEOMATRICAL OPTICS EXERCISE - Advance level Problems35videos
GEOMATRICAL OPTICS
- BOOK - RESONANCECHAPTER - NUCLEAR PHYSICSEXERCISE - Advanced level solutions16videos
NUCLEAR PHYSICS
Similar Questions
Four particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
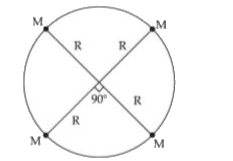 View Solution
View SolutionTwo particles of equal mass (m) move in a circle of radius (r ) under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution
Knowledge Check
- Question 1 - Select One
Two particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
AV=12R√1GmBV=√GM2RCV=12√GmRDV=√4GmR - Question 2 - Select One
Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A√GMRB√2√2GMRC√GMR(1+2√2)D12√GMR(1+2√2) - Question 3 - Select One
Two particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
A12√GmRB√4GMRC12R√1GmD√Gm2R
_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.View SolutionTwo particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionFor particles of equal massses M move along a circle of radius R under th action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
View SolutionFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
View Solution

