Two balls of mass 'm' and 'm10' hang at the two ends of a string that passes through a fixed tube and one of the balls lies in the tube, while the other is outside of the tube. The mass 'm10' is rotating about PQ, as shown in figure. Coefficient of friction between the tube and the ball is '1'. Ball which is insid the tube remains in rest and the time period of revolution of the smaller ball is maximum . Find the angle 'θ' which is made by the string with vertical PQ.
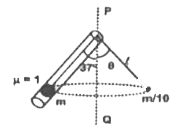
53∘
30∘
60∘
37∘
The correct Answer is:C
Topper's Solved these Questions
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:SECTION (II) : (SUBJECTIVE )
Explore 33 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:SECTION(II) : MCQ ( SINGLE CORRECT)
Explore 47 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:NUMERICAL BASED QUESTIONS
Explore 3 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:NUMERICAL BASES QUESTIONS
Explore 1 Video
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
Similar Questions
A large mass M and a small mass m hang at two ends of a string that passes over a smooth tube as shown in the figure. The mass m moves around a circular path which lies in a horizontal plane. The length of string from the mass m to the top of the tube is l and θ is the 'angle' this length makes with the vertical. What should be the frequency of rotation of mass m, so that the mass M remains stationary?

View SolutionA large mass M and a small mass m hang at the two ends of string passing through a smooth tube. The mass m moves around in a circular path in a horizontal plane. The length of the string from the mass m to the top of the tube of the tube is l and θ is the angle this length makes with the vertical. What should be the frequency of rotation of the mass m so that M remains stationary ?
View Solution
Knowledge Check
A ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
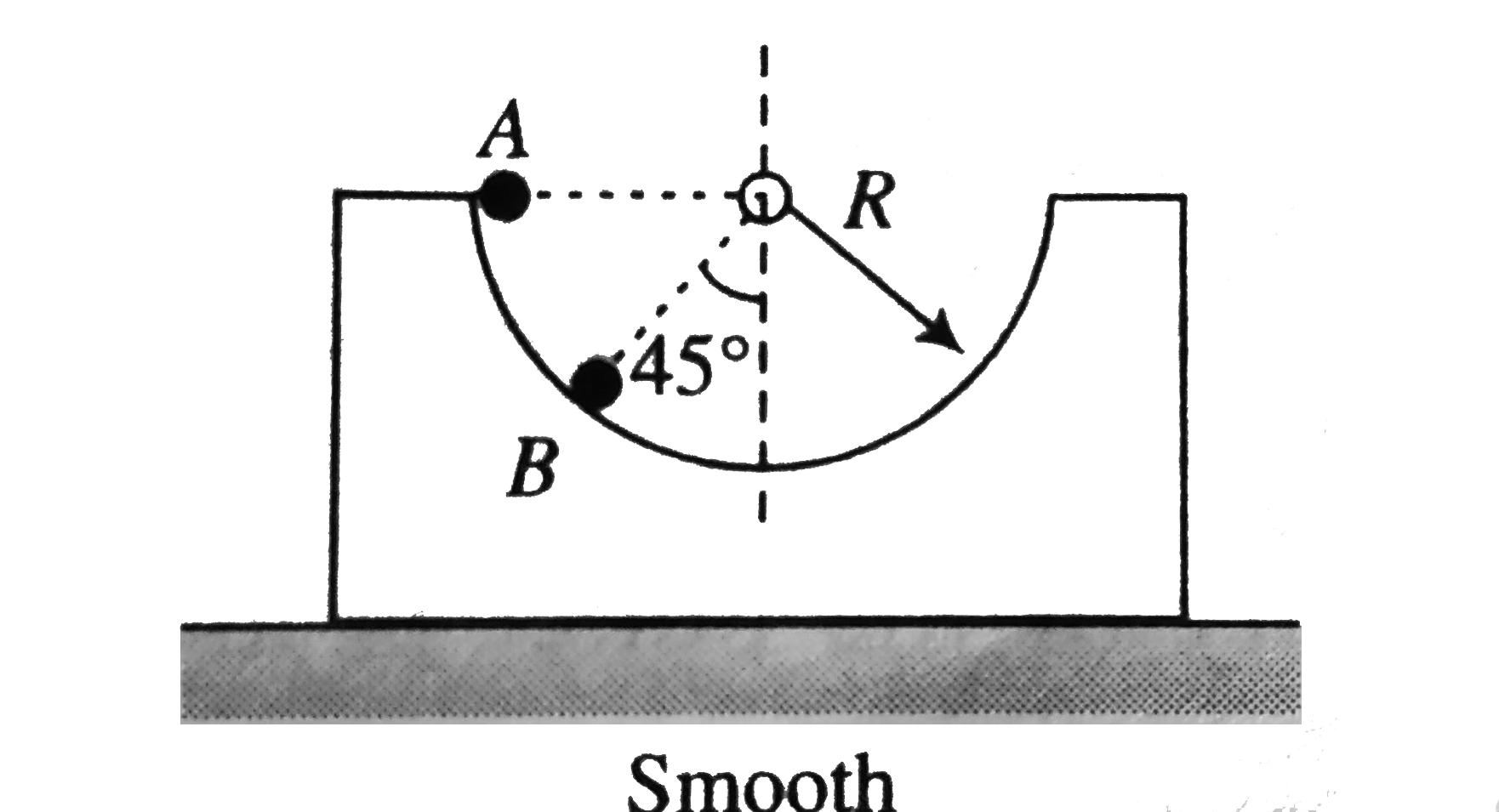 A(a) (gR3√2)1/2B(b) √2gRC(c) (5gR2√3)1/2D(d) √32gR
A(a) (gR3√2)1/2B(b) √2gRC(c) (5gR2√3)1/2D(d) √32gRTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is
 A1B2C3DInfinity
A1B2C3DInfinityTwo balls each of mass 'm' are moving with same velocity v on a smooth surface as shown in figure. If all collisions between the balls and balls with the wall are perfectly elastic, the possible number of collisions between the balls and wall together is
 A1B2C3DInfinity
A1B2C3DInfinity
A ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?

View SolutionA large mass M and a small mass m hang at the two ends of string that passes through a smooth tube as shown in fig. The mass m moves around in a circular path which lies in a horizantal plane. The length of the string from the mass m to the top of the tube is of length l and θ is the angle this length makes with the vertical, what should be the frequency of rotation of the mass m so that M remains stationary if M=16kg,m=4kg,l=1m and g=π2m/s2
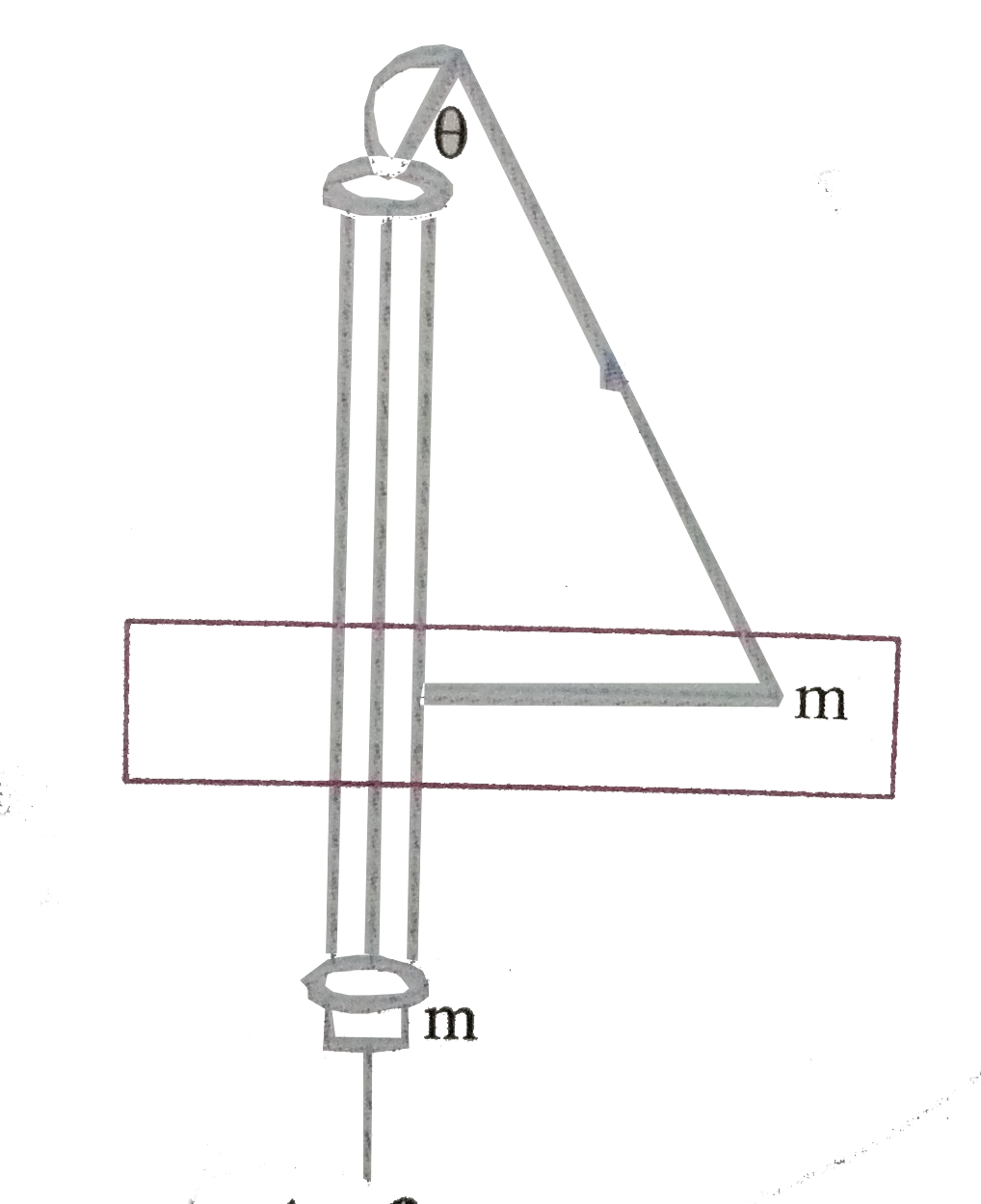
View SolutionA large mass M and a small mass m hang at the two ends of string that passes through a smooth tube as shown in fig. The mass m moves around in a circular peth which lies in a horizantal plane. The length of the stribng from the mass m to the top of the tube is of length l and θ is the angle this length makes with the vertical, what should be the frequency of rotation of the mass m so that M remains stationary if M=16kg,m=4kg,l=1m and g=π2m/s2

View SolutionA small ball of mass m is released in a smooth circular tube as shown in figure. The minimum height h such that bead can complete the circle is
View SolutionRod can rotate about hinge point 'P'. A ball of mass 'm' is projected with a velocity 5v0 in a gravity free space as shown in figure. Collision between the rod and the ball is perfectly elastic. Then find the magnitude of velocity of ball after the collision ( neglect the friction between the ball and the rod during the collision ).
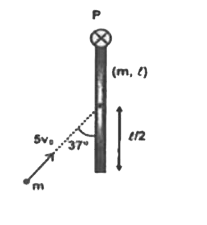
View Solution
