A ball of mass filled with a gas ( whose mass is ) is kept on a frictionless table . A bullet of mass and velocity penetrates the ball , and rests inside at t=0. Assume that the amount of gas emitted during the collision can be neglected. The compressed gas is emitted at a contant velocity relative to the ball and at an even rate k ( k is a positive constant ) .
(a) What is the velocity of the ball after the collision with the bullet ?
(b) Find the velocity of the ball as a function of time. Assume that the emission of gas starts at t=0. What is the final velocity of the ball ?

The correct Answer is:(a) , ( b ) , ( c ) 4.55
Topper's Solved these Questions
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:SECTION(II) : MCQ ( SINGLE CORRECT)
Explore 47 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:MCQ (MULTIPLE CORRECT)
Explore 15 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:SECTION(I): MCQ (SINGLE CORRECT)
Explore 120 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:NUMERICAL BASES QUESTIONS
Explore 1 Video
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
Similar Questions
A heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.
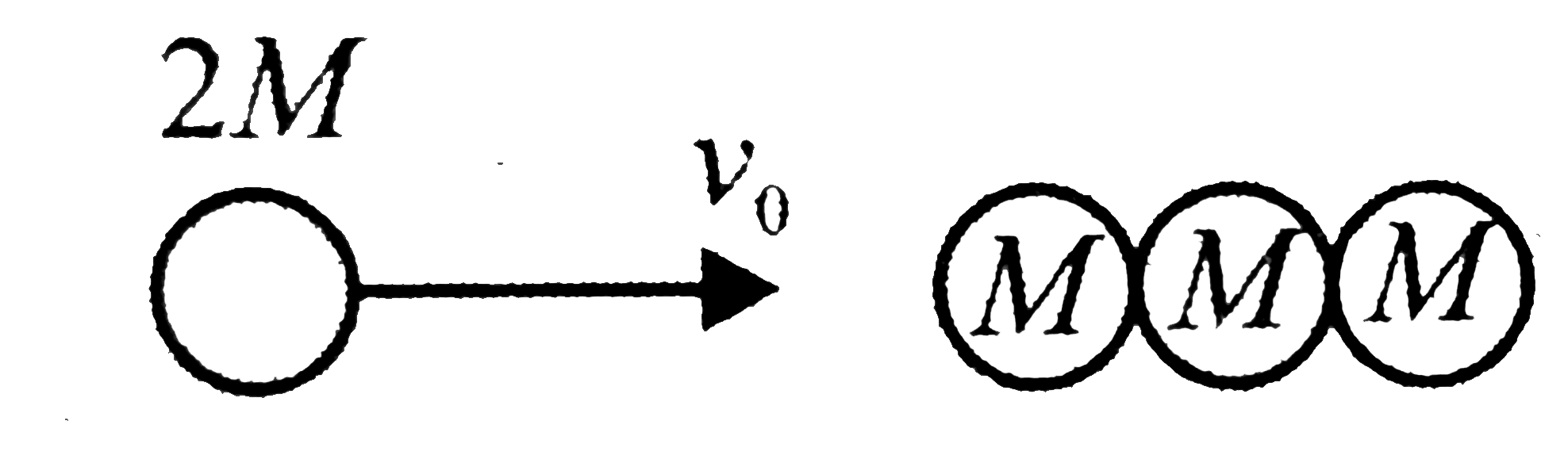
View SolutionA heavy ball of mass 2M moving with a velocity v0 collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.
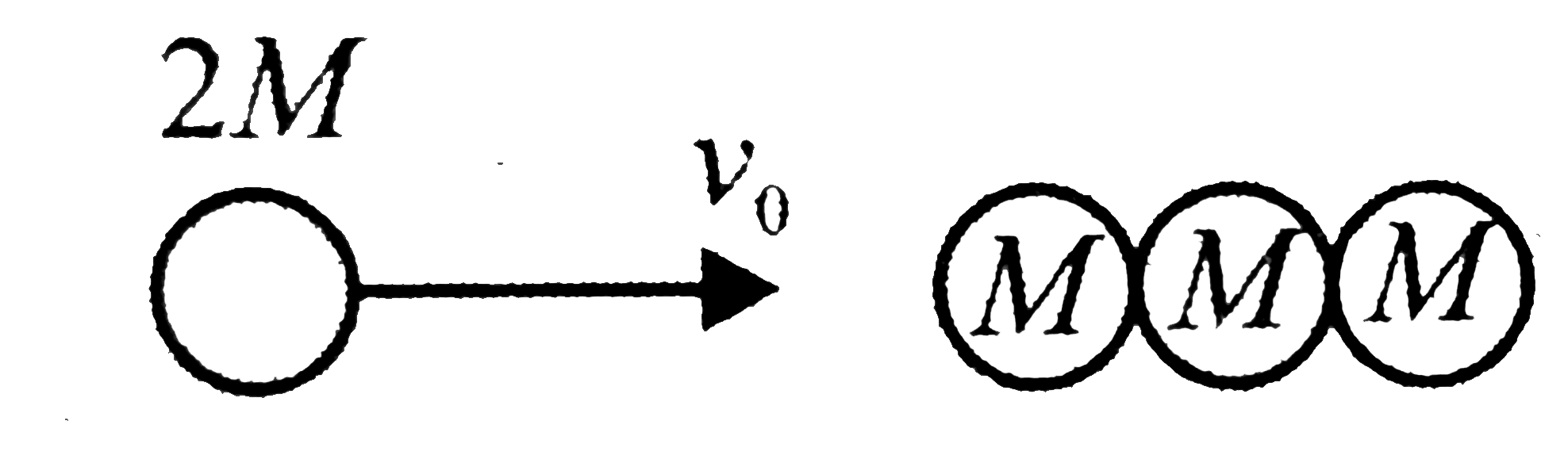
View Solution
Knowledge Check
A ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
Av1=(1−e)u2,v2=(1+e)u2Bv1=(1+e)u2,v2=(1−e)u2Cv1=u2,v2=−u2Dv1=(1+e)u,v2=(1−e)u
A ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA ball of mass m is pushed with a horizontal velocity v0 from one end of a sledge of mass M and length l. if the ball stops after is first collision with the sledge, find the speeds of the ball ad sledge after the second collision of the ball with the sledge.

View SolutionA ball of mass m is pushed with a horizontal velocity v0 from one end of a sledge of mass M and length l. if the ball stops after is first collision with the sledge, find the speeds of the ball ad sledge after the second collision of the ball with the sledge.

View SolutionA ball of mass m moving with velocity u collides head-on which the second ball of mass m at rest. If the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
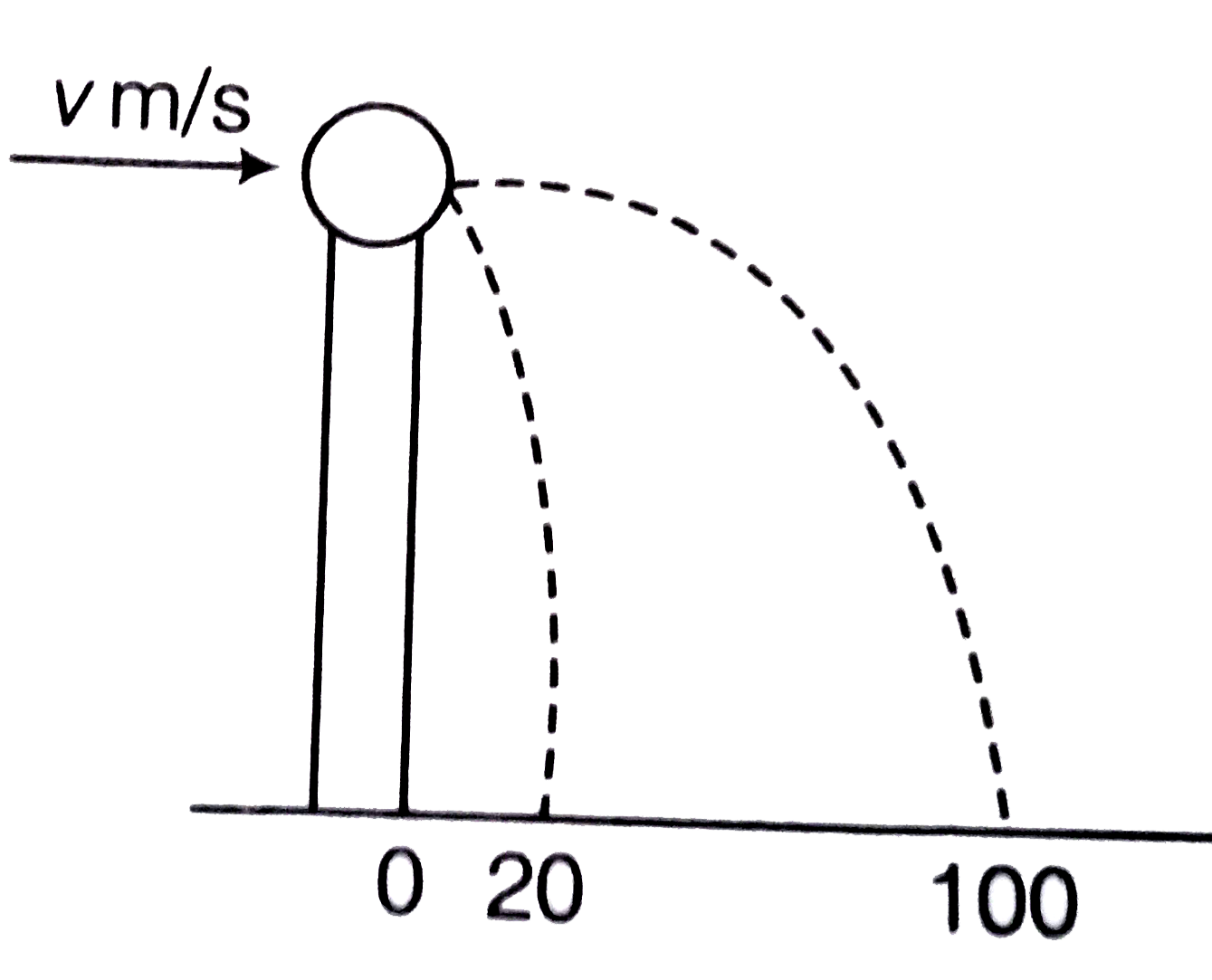
View SolutionA ball of mass 0.2 kg rests on a vertical post of height 5m. A bullet of mass 0.01 kg, travelling with a velocity v m/s in a horizontal direction, hits the centre of the ball. After the collision, the ball and ullet travel independently. The ball hits the ground at a distance of 20 m and the bullet at a distance of 100m from the foot of the post. the initial velocity v of the bullet is
View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View Solution
