It is desired to make a 20Omega coil of wire which has a zero thermal coefficient of resistance. To do this, a carbon resistor of resistance R, is placed in series with an iron resistor of resistance R. The proportions of Iron and carbon are so chosen that $R_{1}, + R_{2} = 20 Ω$ for all temperatures near $20^{\circ} C$ . How large are Ri andR2 ? $(a - (c) = - 0.5 \times 10^{- 3} /^{\circ} C, a_{f e} = 5 \times 10^{- 3} /^{\circ} C)$
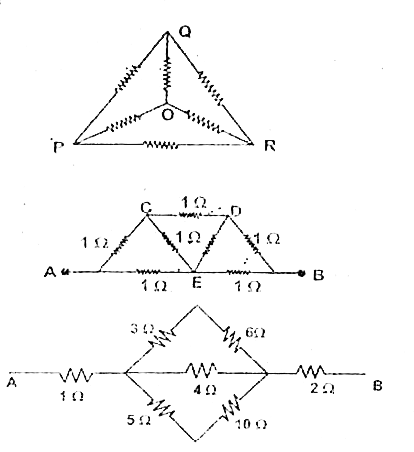
(b) Six equal resistances, each of resistance $4 Ω$ are connected to form the following figure. What is the resistance between any two corners?
(c) In the network shown in figuro, each resistance is $1 Ω$ . What is the effective resistance between A and B.
(d) Find the equivalent resistance between points A and B of the network shown in the given diagram.

Text Solution

Verified by Experts

We need $R_{1} (1 + α_{1} △ t) + R_{2} (1 + α_{2} △ t) = 20$ ,because $R_{1} + R_{2} = 20$ where $△ t = 0$
We must have $R_{1} \propto_{1} R_{2} \propto_{2} w h i t \propto_{1} = - 0.5 \times 10^{- 3} and \propto_{2} = 5 \times 10^{- 3}$
Solving the two equations, $R_{1} + R_{2} = 20$ and $R_{1} = 18.18 Ω and R_{2} = 1.82 Ω$
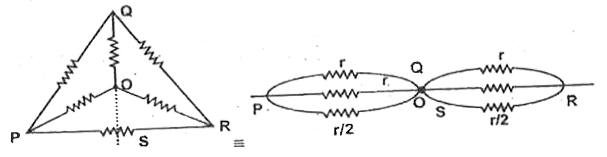
(b) There is a symmetry about the line passing through QO and mid point of PR
$R_{P R} = \frac{r}{2} = 2 Ω$

( c) There is a symmetry about the line passing through E and mid point of CD.

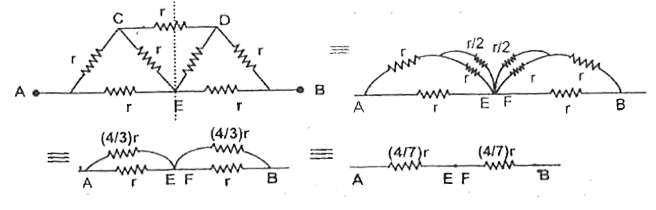
$R_{A B} = \frac{8}{7} r = \frac{8}{7} Ω$
(d) The resistors $3 Ω$ and $6 Ω$ are in series and so are $5 Ω$ and $10 Ω$ resistors. These two series equivalents are in parallel to each other and also to the 4 Hence, the network reduces to the one given in the above figure $R_{e q} = 5.34 Ω$

Updated on:21/07/2023

A resistor of resistance R is connected to a cell internal resistance $5 Ω$ . The value of R is varied from $1 Ω$ to $5 Ω$ . The power consumed by R
Aincreases continuously
Bdecreases continuously
Cfirst decreases then increases
Dfirst increases then decreases
In a series $L C R$ circuit, resistance $R = 10 Ω$ and the impedence $Z = 20 Ω$ the phase difference between the current and the voltage is
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $90^{\circ}$