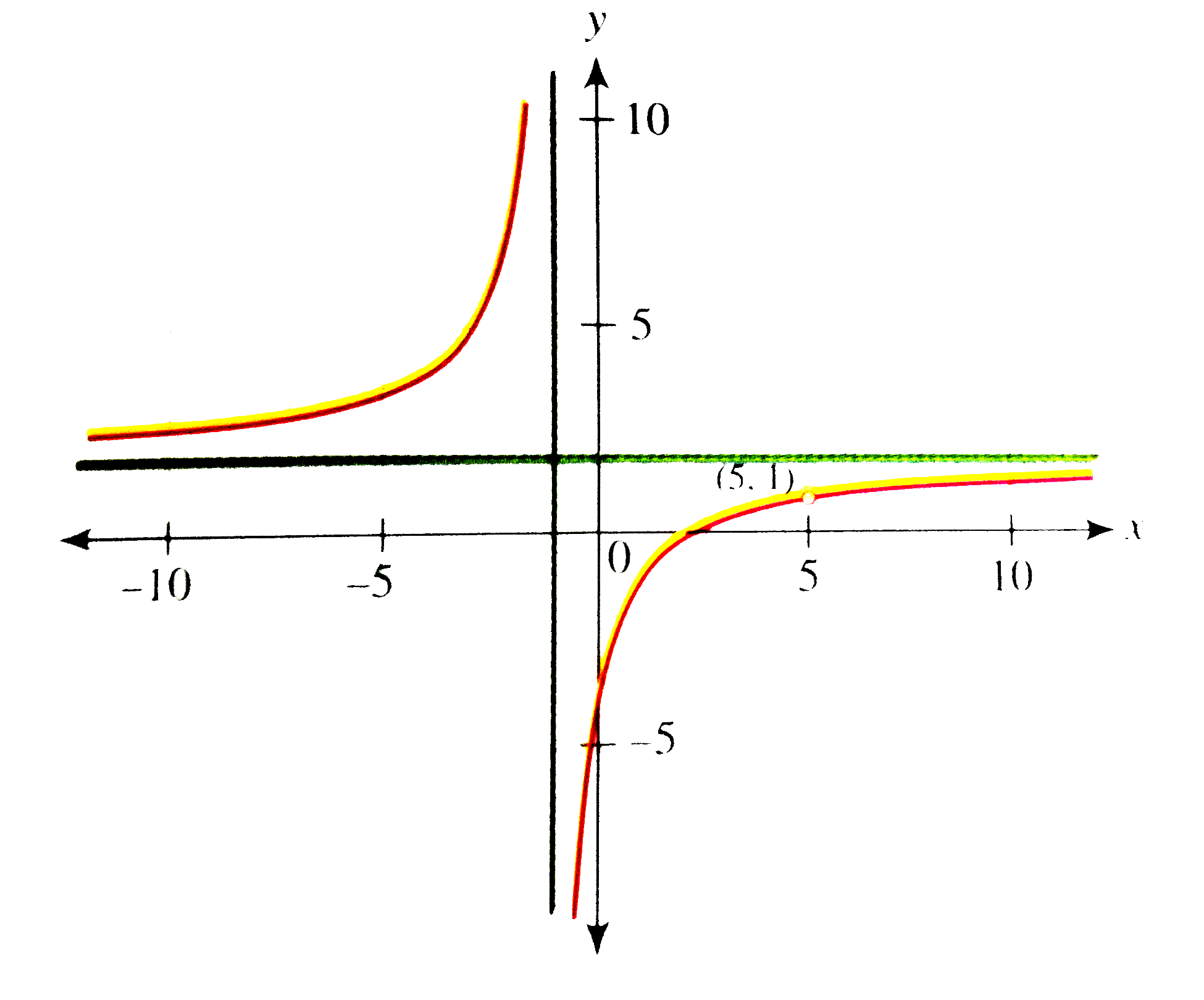
Write a possible rational function h with a hole at x = 5, a vertical asymptote at x = -1, a horizontal asymptote at y = 2 and x-intercept at x = 2.
Since h has a hole at x = 5 , both the numerator and the denominator have a zero at x = 5. Also the vertical asymptote at at x = -1 means the denominator has a zero at x = -1. An x-intercept at x = 2 means the numerator has a zero at x = 2 . Finally, the horizontal asymptote y = 2 means that the numerator and the denominator have equal degree and the ratio of their leading coefficients is equal to 2. Hence
h(x)=2(x−5)(x−2)(x−5)(x+1)
The graph of h is shown below, check the characteristics.
Topper's Solved these Questions
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
Similar Questions
Write a rational function g with vertical asymptotes at x = 3 and x = -3, a horizontal asymptote at y = -4 and with no x-intercept.
View SolutionWrite a possible rational function f that has a vertical asymptote at x = 2, a horizontal asymptote y = 3 and a zero at x = -5. Also draw the graph of the function.
View Solution
Knowledge Check
Equation of asymptotes of xy=7x+5y are
Ax=7, y=5Bx=5, y=7Cxy=35DNone of theseIf length of perpendicular drawn from points of a curve to a straight line approaches zero along an infinite branch of the curve, the line is said to be an asymptote to the curve. For example , y-axis is an asymptote to y=lnx& x-axis is an asymptote to y=e−x.
If limx→0f(x)=e (a finite number) then y=e is an asymptote to y=f(x) . Similarly if limx→0f(x)=α, then y=α is also an asymptote.
If limx→af(x)=∞ or limx→af(x)=−∞, then x=a is a an asymptote to y=f(x).
Number of asymptotes parallel to co -ordinate aces for the function f(x)=(x+1)(x+2)(x−1)(x−2) is equal to :A1B2C3D4If length of perpendicular drawn from points of a curve to a straight line approaches zero along an infinite branch of the curve, the line is said to be an asymptote to the curve. For example , y-axis is an asymptote to y=lnx& x-axis is an asymptote to y=e−x.
If limx→0f(x)=e (a finite number) then y=e is an asymptote to y=f(x) . Similarly if limx→0f(x)=α, then y=α is also an asymptote.
If limx→af(x)=∞ or limx→af(x)=−∞, then x=a is a an asymptote to y=f(x).
Area bounded by y=2xx2+1, it's asymptote and ordinates at points of extremum is equal to (in suare unit)Aln2B2ln2Cln3D2ln3
Write a rational function f with a slant asymptote y=x+4, a vertical asymptote at x = 5 and one of the zeros at x = 2.
View SolutionFind the horizontal asymptote of (x+3)(x−7)(2x−5)
View SolutionThe differential equation of the family of the hyperbola with asymptotes as the lines x+y=1 and x−y=1,
View SolutionThe line x+y+1=0 is an asymptote of x2−y2+x−y−2=0. The other asymptote is
View SolutionIf length of perpendicular drawn from points of a curve to a straight line approaches zero along an infinite branch of the curve, the line is said to be an asymptote to the curve. For example , y-axis is an asymptote to y=lnx& x-axis is an asymptote to y=e−x.
If limx→0f(x)=e (a finite number) then y=e is an asymptote to y=f(x) . Similarly if limx→0f(x)=α, then y=α is also an asymptote.
If limx→af(x)=∞ or limx→af(x)=−∞, then x=a is a an asymptote to y=f(x).
Area bounded by y=x2e−x and it's asymptote in first quadrant is equal to (in square unit)
View Solution
