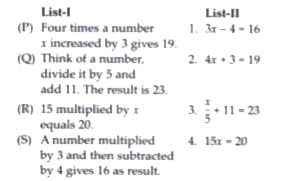Match the statements/expressions given in List ( with the value given in List II.

Text Solution
The correct Answer is:4
a. Let f(x)=ax2+bx(∵f(0)=0)
Given ∫10f(x)dx=1
=2a+3b=6
=(a,b)=(0,2) and (3,0)
b. f(x)=sin(x2)+cos(x2)
=√2cos(x2−π4)
For maximum value x2−π4=2nπ,nεZ
⇒x2=2nπ+π4,nεZ
⇒x=±√x4±√9π4 as xε[−√13,√13]
c. I=∫2−23x2(1+ex)dx...............1
=∫2−23(−x)21+e−xdx
∴I=∫2−2ex(3x)2ex+1dx............2
Addding 1 and 2
⇒I+I=∫2−23x2(1+ex)dx+∫2−2ex(3x2)ex+1dx
=∫2−23x2dx=2∫203x2dx=16
⇒I=8
d. We have I=∫1/21/2cos2x.log(1+x1−x)dx∫1/20cos2x.log(1+x1−x)dx
Let f(x)=cos2xI(1+x1−x)
∴f(−x)=cos(−2x)In(1−x1+x)
=−cos(2x)In(1+x1−x)=−f(x)
Thus, f(x) is an odd function.
⇒I=0
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Match the statements/expressions given in List I with the values given in List II.
 AabcdsrqpBabcdqsrpCabcdsrpqDabcdqspr
AabcdsrqpBabcdqsrpCabcdsrpqDabcdqsprMatch the quantities given in List-I with the units given in List-II
 APQRS4321BPQRS3421CPQRS2314DPQRS1234
APQRS4321BPQRS3421CPQRS2314DPQRS1234Match the compounds given in list I with their characterstics reactions in list II
 A1-a,2-c,3-d,4-bB1-c,2-d,3-b,4-aC1-a,2-b,3-c,4-dD1-d,2-a,3-b,4-c
A1-a,2-c,3-d,4-bB1-c,2-d,3-b,4-aC1-a,2-b,3-c,4-dD1-d,2-a,3-b,4-c
Match the statements/expressions in List I statements/expression in List II

View SolutionMatch the quantities given in List-I to the respective ratios given in List-II.
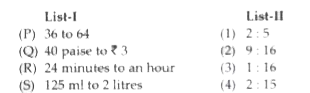
View SolutionMatch the compounds given in list I with their characterstics reactions in list II

View SolutionMatch structures given in list I with names given in list II and then select the correct answer from the codes given below the list

View Solution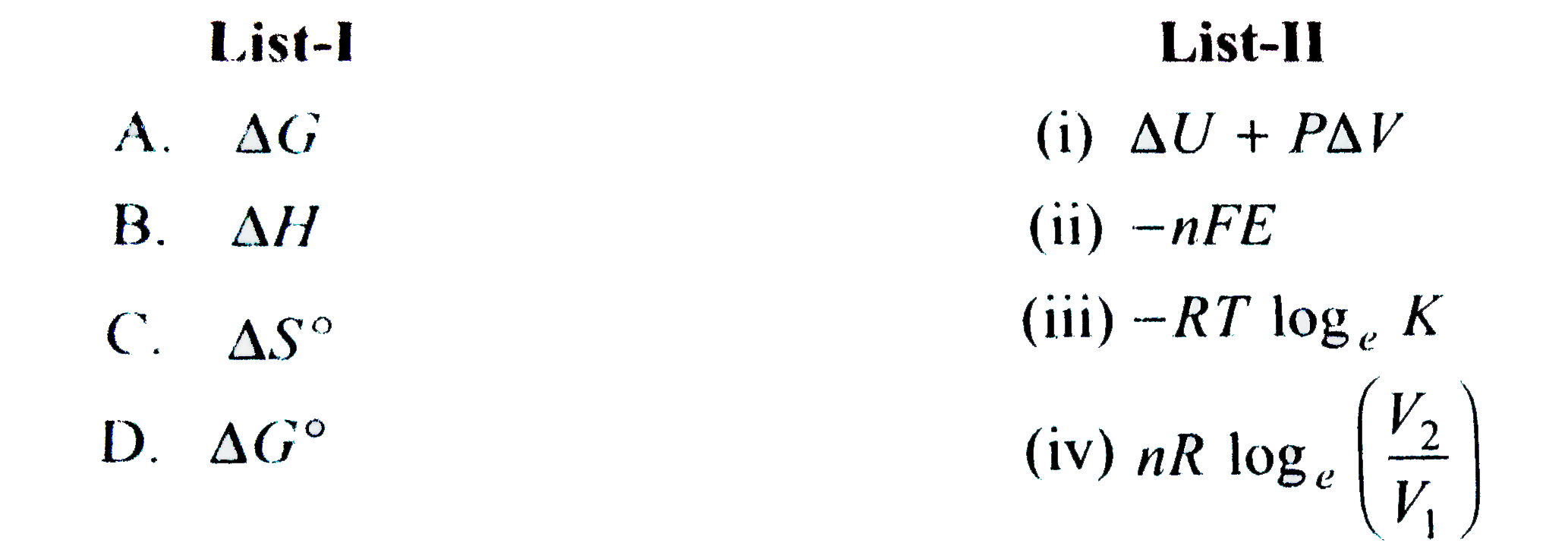 ltBrgt Match the physical changes in List-I with their relations given in List-II:
ltBrgt Match the physical changes in List-I with their relations given in List-II:
View Solution